Exploring the Universe with SNAD: Anomaly Detection in Astronomy

SNAD is an international project with a primary focus on detecting astronomical anomalies within large-scale surveys, using active learning and other machine learning algorithms. The work carried out by SNAD not only contributes to the discovery and classification of various astronomical phenomena but also enhances our understanding and implementation of machine learning techniques within the field of astrophysics. This paper provides a review of the SNAD project and summarizes the advancements and achievements made by the team over several years.

Active Anomaly Detection for time-domain discoveries

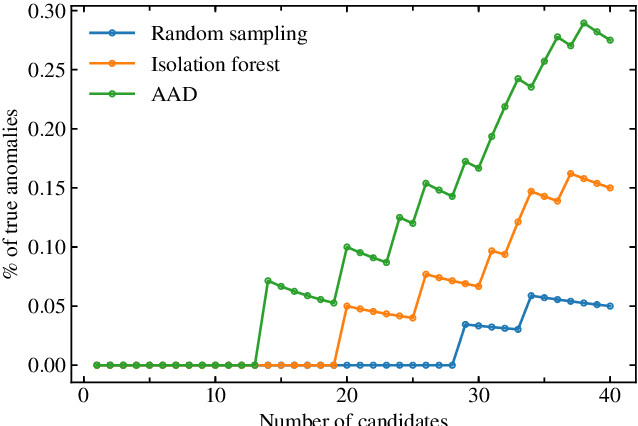
We present the first application of adaptive machine learning to the identification of anomalies in a data set of non-periodic astronomical light curves. The method follows an active learning strategy where highly informative objects are selected to be labelled. This new information is subsequently used to improve the machine learning model, allowing its accuracy to evolve with the addition of every new classification. For the case of anomaly detection, the algorithm aims to maximize the number of real anomalies presented to the expert by slightly modifying the decision boundary of a traditional isolation forest in each iteration. As a proof of concept, we apply the Active Anomaly Discovery (AAD) algorithm to light curves from the Open Supernova Catalog and compare its results to those of a static Isolation Forest (IF). For both methods, we visually inspected objects within 2% highest anomaly scores. We show that AAD was able to identify 80% more true anomalies than IF. This result is the first evidence that AAD algorithms can play a central role in the search for new physics in the era of large scale sky surveys.

Maximum likelihood estimation for disk image parameters

We present a novel technique for estimating disc parameters from its 2D image. It is based on the maximal likelihood approach utilising both edge coordinates and the image intensity gradients. We emphasise the following advantages of our likelihood model. It has closed-form formulae for parameter estimating, therefore requiring less computational resources than iterative algorithms. The likelihood model naturally distinguishes the outer and inner annulus edges. The proposed technique was evaluated on both synthetic and real data.