Link Streams as a Generalization of Graphs and Time Series

A link stream is a set of possibly weighted triplets (t, u, v) modeling that u and v interacted at time t. Link streams offer an effective model for datasets containing both temporal and relational information, making their proper analysis crucial in many applications. They are commonly regarded as sequences of graphs or collections of time series. Yet, a recent seminal work demonstrated that link streams are more general objects of which graphs are only particular cases. It therefore started the construction of a dedicated formalism for link streams by extending graph theory. In this work, we contribute to the development of this formalism by showing that link streams also generalize time series. In particular, we show that a link stream corresponds to a time-series extended to a relational dimension, which opens the door to also extend the framework of signal processing to link streams. We therefore develop extensions of numerous signal concepts to link streams: from elementary ones like energy, correlation, and differentiation, to more advanced ones like Fourier transform and filters.

A Frequency-Structure Approach for Link Stream Analysis

A link stream is a set of triplets $(t, u, v)$ indicating that $u$ and $v$ interacted at time $t$. Link streams model numerous datasets and their proper study is crucial in many applications. In practice, raw link streams are often aggregated or transformed into time series or graphs where decisions are made. Yet, it remains unclear how the dynamical and structural information of a raw link stream carries into the transformed object. This work shows that it is possible to shed light into this question by studying link streams via algebraically linear graph and signal operators, for which we introduce a novel linear matrix framework for the analysis of link streams. We show that, due to their linearity, most methods in signal processing can be easily adopted by our framework to analyze the time/frequency information of link streams. However, the availability of linear graph methods to analyze relational/structural information is limited. We address this limitation by developing (i) a new basis for graphs that allow us to decompose them into structures at different resolution levels; and (ii) filters for graphs that allow us to change their structural information in a controlled manner. By plugging-in these developments and their time-domain counterpart into our framework, we are able to (i) obtain a new basis for link streams that allow us to represent them in a frequency-structure domain; and (ii) show that many interesting transformations to link streams, like the aggregation of interactions or their embedding into a euclidean space, can be seen as simple filters in our frequency-structure domain.

A logical approach for temporal and multiplex networks analysis

Many systems generate data as a set of triplets (a, b, c): they may represent that user a called b at time c or that customer a purchased product b in store c. These datasets are traditionally studied as networks with an extra dimension (time or layer), for which the fields of temporal and multiplex networks have extended graph theory to account for the new dimension. However, such frameworks detach one variable from the others and allow to extend one same concept in many ways, making it hard to capture patterns across all dimensions and to identify the best definitions for a given dataset. This extended abstract overrides this vision and proposes a direct processing of the set of triplets. In particular, our work shows that a more general analysis is possible by partitioning the data and building categorical propositions that encode informative patterns. We show that several concepts from graph theory can be framed under this formalism and leverage such insights to extend the concepts to data triplets. Lastly, we propose an algorithm to list propositions satisfying specific constraints and apply it to a real world dataset.

A Local Updating Algorithm for Personalized PageRank via Chebyshev Polynomials

The personalized PageRank algorithm is one of the most versatile tools for the analysis of networks. In spite of its ubiquity, maintaining personalized PageRank vectors when the underlying network constantly evolves is still a challenging task. To address this limitation, this work proposes a novel distributed algorithm to locally update personalized PageRank vectors when the graph topology changes. The proposed algorithm is based on the use of Chebyshev polynomials and a novel update equation that encompasses a large family of PageRank-based methods. In particular, the algorithm has the following advantages: (i) it has faster convergence speed than state-of-the-art alternatives for local PageRank updating; and (ii) it can update the solution of recent generalizations of PageRank for which no updating algorithms have been developed. Experiments in a real-world temporal network of an autonomous system validate the effectiveness of the proposed algorithm.

Full Bitcoin Blockchain Data Made Easy

Despite the fact that it is publicly available, collecting and processing the full bitcoin blockchain data is not trivial. Its mere size, history, and other features indeed raise quite specific challenges, that we address in this paper. The strengths of our approach are the following: it relies on very basic and standard tools, which makes the procedure reliable and easily reproducible; it is a purely lossless procedure ensuring that we catch and preserve all existing data; it provides additional indexing that makes it easy to further process the whole data and select appropriate subsets of it. We present our procedure in details and illustrate its added value on large-scale use cases, like address clustering. We provide an implementation online, as well as the obtained dataset.

Computing Betweenness Centrality in Link Streams

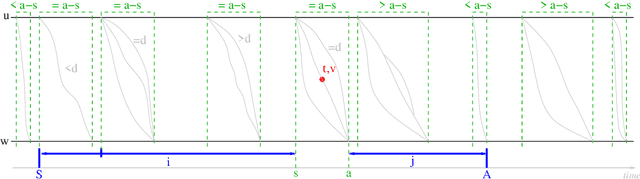
Betweeness centrality is one of the most important concepts in graph analysis. It was recently extended to link streams, a graph generalization where links arrive over time. However, its computation raises non-trivial issues, due in particular to the fact that time is considered as continuous. We provide here the first algorithms to compute this generalized betweenness centrality, as well as several companion algorithms that have their own interest. They work in polynomial time and space, we illustrate them on typical examples, and we provide an implementation.

A general graph-based framework for top-N recommendation using content, temporal and trust information

Recommending appropriate items to users is crucial in many e-commerce platforms that contain implicit data as users' browsing, purchasing and streaming history. One common approach consists in selecting the N most relevant items to each user, for a given N, which is called top-N recommendation. To do so, recommender systems rely on various kinds of information, like item and user features, past interest of users for items, browsing history and trust between users. However, they often use only one or two such pieces of information, which limits their performance. In this paper, we design and implement GraFC2T2, a general graph-based framework to easily combine and compare various kinds of side information for top-N recommendation. It encodes content-based features, temporal and trust information into a complex graph, and uses personalized PageRank on this graph to perform recommendation. We conduct experiments on Epinions and Ciao datasets, and compare obtained performances using F1-score, Hit ratio and MAP evaluation metrics, to systems based on matrix factorization and deep learning. This shows that our framework is convenient for such explorations, and that combining different kinds of information indeed improves recommendation in general.

Link Stream Graph for Temporal Recommendations

Several researches on recommender systems are based on explicit rating data, but in many real world e-commerce platforms, ratings are not always available, and in those situations, recommender systems have to deal with implicit data such as users' purchase history, browsing history and streaming history. In this context, classical bipartite user-item graphs (BIP) are widely used to compute top-N recommendations. However, these graphs have some limitations, particularly in terms of taking temporal dynamic into account. This is not good because users' preference change over time. To overcome this limit, the Session-based Temporal Graph (STG) was proposed by Xiang et al. to combine long- and short-term preferences in a graph-based recommender system. But in the STG, time is divided into slices and therefore considered discontinuously. This approach loses details of the real temporal dynamics of user actions. To address this challenge, we propose the Link Stream Graph (LSG) which is an extension of link stream representation proposed by Latapy et al. and which allows to model interactions between users and items by considering time continuously. Experiments conducted on four real world implicit datasets for temporal recommendation, with 3 evaluation metrics, show that LSG is the best in 9 out of 12 cases compared to BIP and STG which are the most used state-of-the-art recommender graphs.

Stream Graphs and Link Streams for the Modeling of Interactions over Time

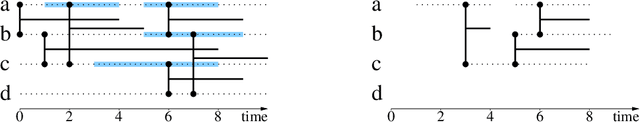
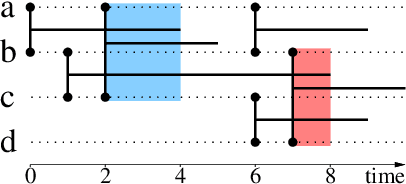
Graph theory provides a language for studying the structure of relations, and it is often used to study interactions over time too. However, it poorly captures the both temporal and structural nature of interactions, that calls for a dedicated formalism. In this paper, we generalize graph concepts in order to cope with both aspects in a consistent way. We start with elementary concepts like density, clusters, or paths, and derive from them more advanced concepts like cliques, degrees, clustering coefficients, or connected components. We obtain a language to directly deal with interactions over time, similar to the language provided by graphs to deal with relations. This formalism is self-consistent: usual relations between different concepts are preserved. It is also consistent with graph theory: graph concepts are special cases of the ones we introduce. This makes it easy to generalize higher-level objects such as quotient graphs, line graphs, k-cores, and centralities. This paper also considers discrete versus continuous time assumptions, instantaneous links, and extensions to more complex cases.