Matthieu Bellucci
ZeLiC and ZeChipC: Time Series Interpolation Methods for Lebesgue or Event-based Sampling
Jun 06, 2019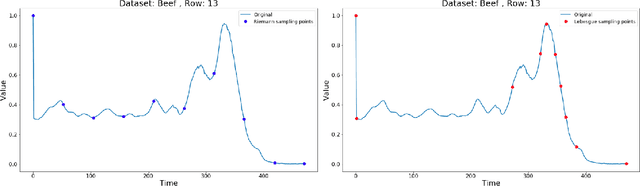
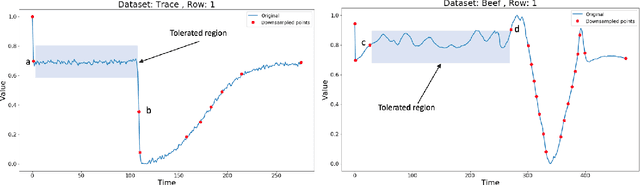
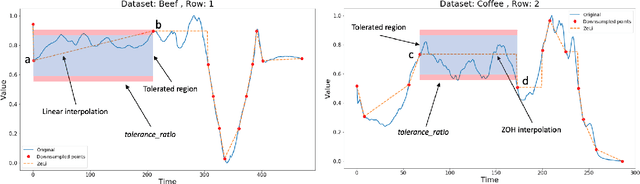
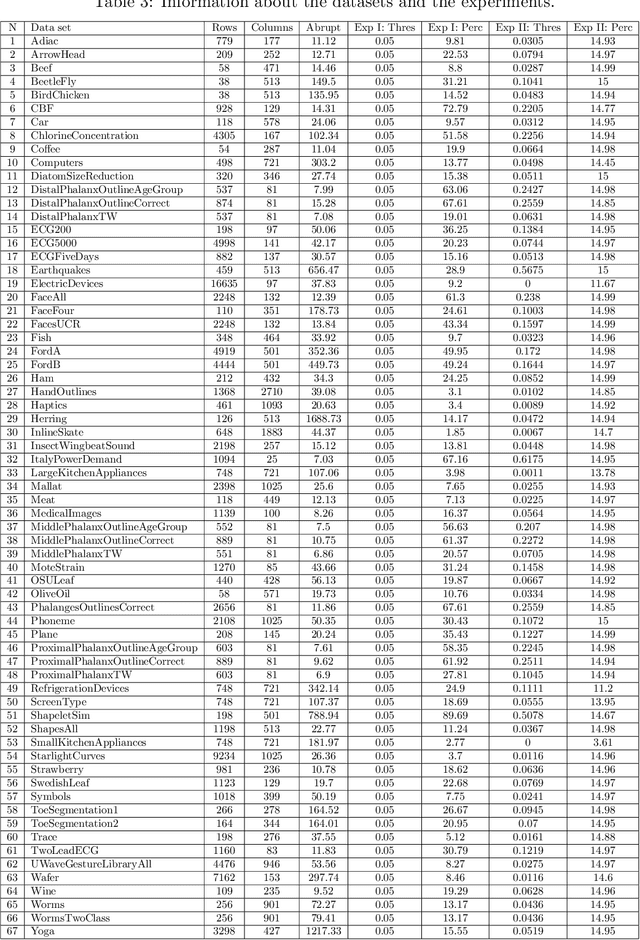
Abstract:Lebesgue sampling is based on collecting information depending on the values of the signal. Although the interpolation methods for periodic sampling have been a topic of research for a long time, there is a lack of study in methods capable of taking advantage of the Lebesgue sampling characteristics to reconstruct time series more accurately. Indeed, Lebesgue sampling contains additional information about the shape of the signal in-between two sampled points. Using this information would allow us to generate an interpolated signal closer to the original one. That is to say, the average distance between the interpolated signal and the original signal will be smaller than a signal interpolated with other interpolation methods. In this paper, we propose two novel time series interpolation methods specifically designed for Lebesgue sampling called ZeLiC and ZeChipC. ZeLiC is an algorithm that combines both Zero-order hold interpolation and Linear interpolation to reconstruct time series. ZeChipC is a similar idea, it is a combination of Zero-order hold and PCHIP interpolation. Zero-order hold interpolation is favourable for interpolating abrupt changes while Linear and PCHIP interpolation are more suitable for smooth transitions. In order to apply one method or the other, we have introduced a new concept called tolerated region. ZeLiC and ZeChipC include a new functionality to adapt the reconstructed signal to concave/convex regions. The proposed methods have been compared with the state-of-the-art interpolation methods using Lebesgue sampling and have offered higher average performance. Additionally, we have compared the performance of the methods using both Riemann and Lebesgue sampling using an approximate number of sampled points. The performance of the combination "Lebesgue sampling with ZeChipC interpolation method" is clearly much better than any other combination.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge