Automotive Radar Online Channel Imbalance Estimation via NLMS

Automotive radars are one of the essential enablers of advanced driver assistance systems (ADASs). Continuous monitoring of the functional safety and reliability of automotive radars is a crucial requirement to prevent accidents and increase road safety. One of the most critical aspects to monitor in this context is radar channel imbalances, as they are a key parameter regarding the reliability of the radar. These imbalances may originate from several parameter variations or hardware fatigues, e.g., a solder ball break (SBB), and may affect some radar processing steps, such as the angle of arrival estimation. In this work, a novel method for online estimation of automotive radar channel imbalances is proposed. The proposed method exploits a normalized least mean squares (NLMS) algorithm as a block in the processing chain of the radar to estimate the channel imbalances. The input of this block is the detected targets in the range-Doppler map of the radar on the road without any prior knowledge on the angular parameters of the targets. This property in combination with low computational complexity of the NLMS, makes the proposed method suitable for online channel imbalance estimation, in parallel to the normal operation of the radar. Furthermore, it features reduced dependency on specific targets of interest and faster update rates of the channel imbalance estimation compared to the majority of state-of-the-art methods. This improvement is achieved by allowing for multiple targets in the angular spectrum, whereas most other methods are restricted to only single targets in the angular spectrum. The performance of the proposed method is validated using various simulation scenarios and is supported by measurement results.

Optimum and Adaptive Complex-Valued Bilinear Filters

The identification of nonlinear systems is a frequent task in digital signal processing. Such nonlinear systems may be grouped into many sub-classes, whereby numerous nonlinear real-world systems can be approximated as bilinear (BL) models. Therefore, various optimum and adaptive BL filters have been introduced in recent years. Further, in many applications such as communications and radar, complex-valued (CV) BL systems in combination with CV signals may occur. Hence, in this work, we investigate the extension of real-valued (RV) BL filters to CV BL filters. First, we derive CV BL filters by applying two or four RV BL filters, and compare them with respect to their computational complexity and performance. Second, we introduce novel fully CV BL filters, such as the CV BL Wiener filter (WF), the CV BL least squares (LS) filter, the CV BL least mean squares (LMS) filter, the CV BL normalized LMS (NLMS) filter, and the CV BL recursive least squares (RLS) filter. Finally, these filters are applied to identify multiple-input-single-output (MISO) systems and Hammerstein models.

Tx and Rx IQ Imbalance Compensation for JCAS in 5G NR

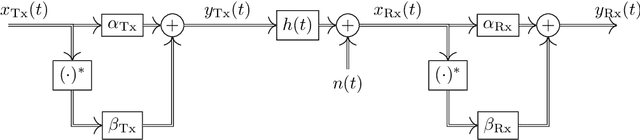
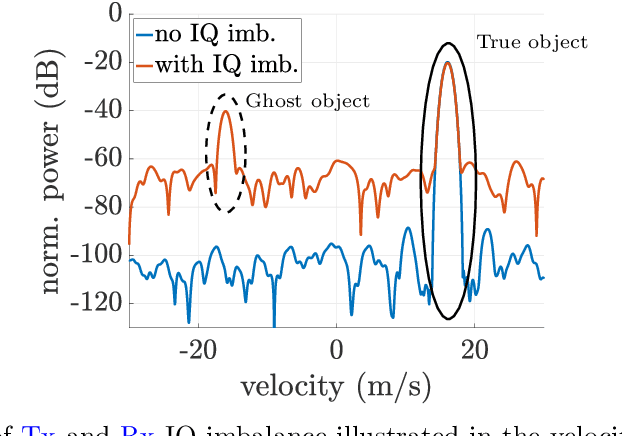
Beside traditional communications, joint communications and sensing (JCAS) is gaining increasing relevance as a key enabler for next-generation wireless systems. The ability to accurately transmit and receive data is the basis for high-speed communications and precise sensing, where a fundamental requirement is an accurate in-phase (I) and quadrature-phase (Q) modulation. For sensing, imperfections in IQ modulation lead to two critical issues in the range-Doppler-map (RDM) in form of an increased noise floor and the presence of ghost objects, degrading the accuracy and reliability of the information in the RDM. This paper presents a low-complex estimation and compensation method to mitigate the IQ imbalance effects. This is achieved by utilizing, amongst others, the leakage signal, which is the direct signal from the transmitter to the receiver path, and is typically the strongest signal component in the RDM. The parameters of the IQ imbalance suppression structure are estimated based on a mixed complex-/real-valued bilinear filter approach, that considers IQ imbalance in the transmitter and the receiver of the JCAS-capable user equipment (UE). The UE uses a 5G New Radio (NR)-compliant orthogonal frequency-division multiplexing (OFDM) waveform with the system configuration assumed to be predefined from the communication side. To assess the effectiveness of the proposed approach, simulations are conducted, illustrating the performance in the suppression of IQ imbalance introduced distortions in the RDM.

Bi-Linear Homogeneity Enforced Calibration for Pipelined ADCs

Pipelined analog-to-digital converters (ADCs) are key enablers in many state-of-the-art signal processing systems with high sampling rates. In addition to high sampling rates, such systems often demand a high linearity. To meet these challenging linearity requirements, ADC calibration techniques were heavily investigated throughout the past decades. One limitation in ADC calibration is the need for a precisely known test signal. In our previous work, we proposed the homogeneity enforced calibration (HEC) approach, which circumvents this need by consecutively feeding a test signal and a scaled version of it into the ADC. The calibration itself is performed using only the corresponding output samples, such that the test signal can remain unknown. On the downside, the HEC approach requires the option to accurately scale the test signal, impeding an on-chip implementation. In this work, we provide a thorough analysis of the HEC approach, including the effects of an inaccurately scaled test signal. Furthermore, the bi-linear homogeneity enforced calibration (BL-HEC) approach is introduced and suggested to account for an inaccurate scaling and, therefore, to facilitate an on-chip implementation. In addition, a comprehensive stability and convergence analysis of the BL-HEC approach is carried out. Finally, we verify our concept with simulations.

Homogeneity Enforced Calibration of Stage Nonidealities for Pipelined ADCs

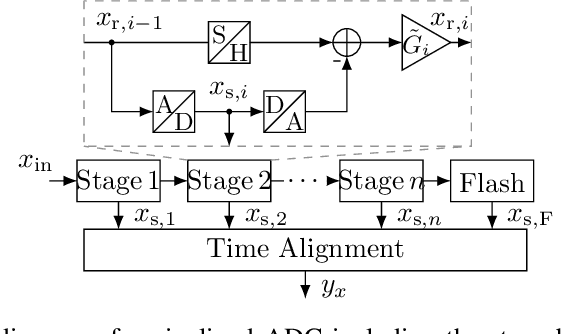
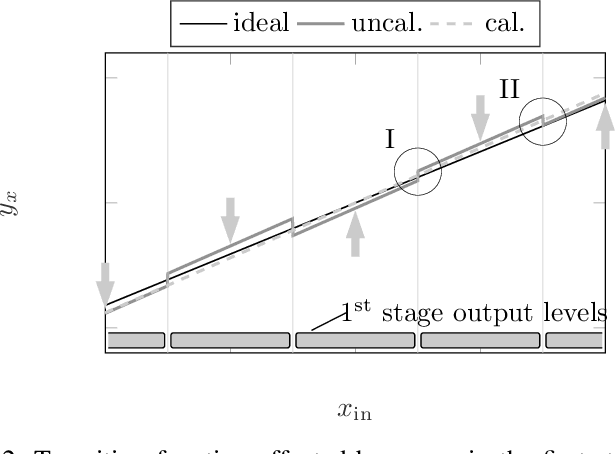
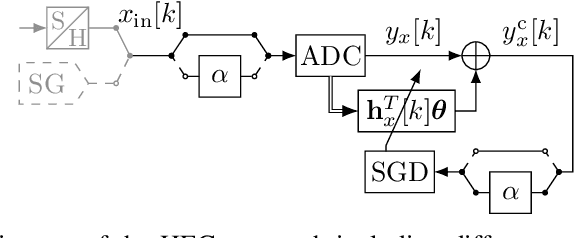
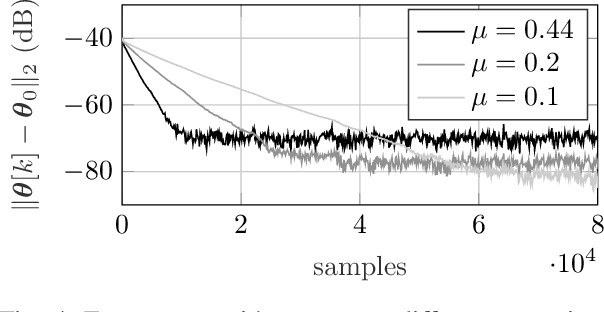
Pipelined analog-to-digital converters (ADCs) are fundamental components of various signal processing systems requiring high sampling rates and a high linearity. Over the past years, calibration techniques have been intensively investigated to increase the linearity. In this work, we propose an equalization-based calibration technique which does not require knowledge of the ADC input signal for calibration. For that, a test signal and a scaled version of it are fed into the ADC sequentially, while only the corresponding output samples are used for calibration. Several test signal sources are possible, such as a signal generator (SG) or the system application (SA) itself. For the latter case, the presented method corresponds to a background calibration technique. Thus, slowly changing errors are tracked and calibrated continuously. Because of the low computational complexity of the calibration technique, it is suitable for an on-chip implementation. Ultimately, this work contains an analysis of the stability and convergence behavior as well as simulation results.