Enhancing Dynamic CT Image Reconstruction with Neural Fields Through Explicit Motion Regularizers

Image reconstruction for dynamic inverse problems with highly undersampled data poses a major challenge: not accounting for the dynamics of the process leads to a non-realistic motion with no time regularity. Variational approaches that penalize time derivatives or introduce motion model regularizers have been proposed to relate subsequent frames and improve image quality using grid-based discretization. Neural fields offer an alternative parametrization of the desired spatiotemporal quantity with a deep neural network, a lightweight, continuous, and biased towards smoothness representation. The inductive bias has been exploited to enforce time regularity for dynamic inverse problems resulting in neural fields optimized by minimizing a data-fidelity term only. In this paper we investigate and show the benefits of introducing explicit PDE-based motion regularizers, namely, the optical flow equation, in 2D+time computed tomography for the optimization of neural fields. We also compare neural fields against a grid-based solver and show that the former outperforms the latter.

Deep smoothness WENO scheme for two-dimensional hyperbolic conservation laws: A deep learning approach for learning smoothness indicators

In this paper, we introduce an improved version of the fifth-order weighted essentially non-oscillatory (WENO) shock-capturing scheme by incorporating deep learning techniques. The established WENO algorithm is improved by training a compact neural network to adjust the smoothness indicators within the WENO scheme. This modification enhances the accuracy of the numerical results, particularly near abrupt shocks. Unlike previous deep learning-based methods, no additional post-processing steps are necessary for maintaining consistency. We demonstrate the superiority of our new approach using several examples from the literature for the two-dimensional Euler equations of gas dynamics. Through intensive study of these test problems, which involve various shocks and rarefaction waves, the new technique is shown to outperform traditional fifth-order WENO schemes, especially in cases where the numerical solutions exhibit excessive diffusion or overshoot around shocks.

PINN Training using Biobjective Optimization: The Trade-off between Data Loss and Residual Loss

Physics informed neural networks (PINNs) have proven to be an efficient tool to represent problems for which measured data are available and for which the dynamics in the data are expected to follow some physical laws. In this paper, we suggest a multiobjective perspective on the training of PINNs by treating the data loss and the residual loss as two individual objective functions in a truly biobjective optimization approach. As a showcase example, we consider COVID-19 predictions in Germany and built an extended susceptibles-infected-recovered (SIR) model with additionally considered leaky-vaccinated and hospitalized populations (SVIHR model) to model the transition rates and to predict future infections. SIR-type models are expressed by systems of ordinary differential equations (ODEs). We investigate the suitability of the generated PINN for COVID-19 predictions and compare the resulting predicted curves with those obtained by applying the method of non-standard finite differences to the system of ODEs and initial data. The approach is applicable to various systems of ODEs that define dynamical regimes. Those regimes do not need to be SIR-type models, and the corresponding underlying data sets do not have to be associated with COVID-19.

Stochastic Primal-Dual Three Operator Splitting with Arbitrary Sampling and Preconditioning

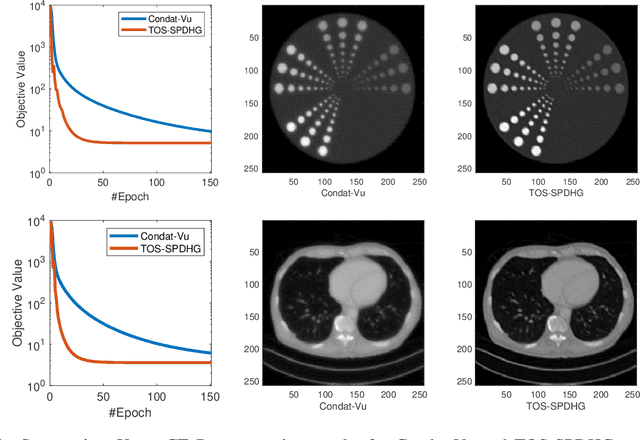
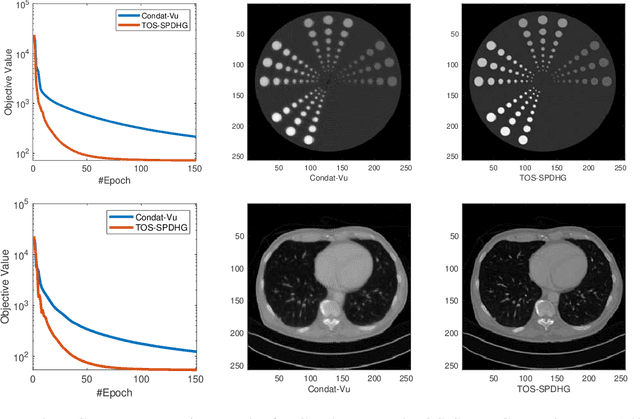
In this work we propose a stochastic primal-dual preconditioned three-operator splitting algorithm for solving a class of convex three-composite optimization problems. Our proposed scheme is a direct three-operator splitting extension of the SPDHG algorithm [Chambolle et al. 2018]. We provide theoretical convergence analysis showing ergodic O(1/K) convergence rate, and demonstrate the effectiveness of our approach in imaging inverse problems.