PINN Training using Biobjective Optimization: The Trade-off between Data Loss and Residual Loss

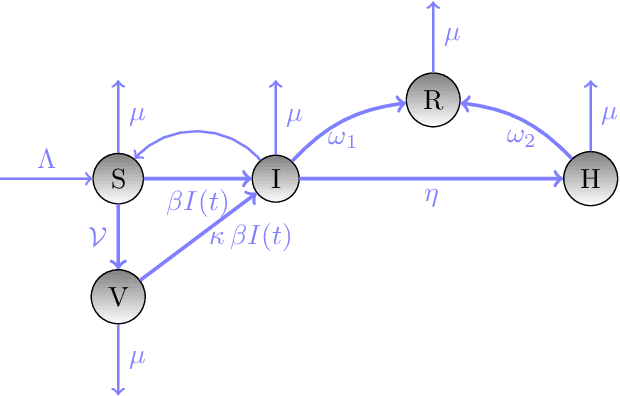
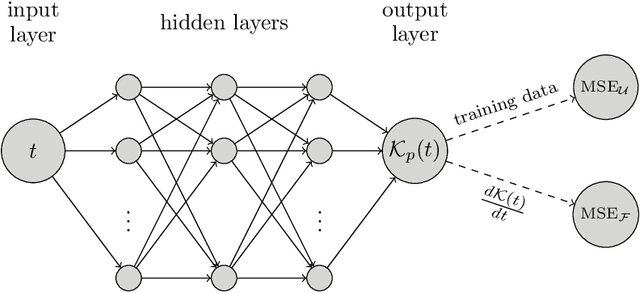
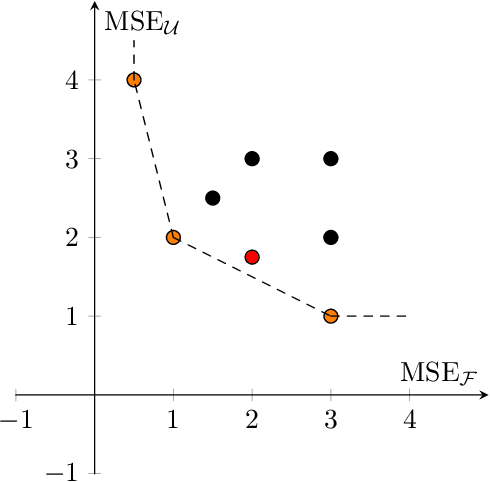
Physics informed neural networks (PINNs) have proven to be an efficient tool to represent problems for which measured data are available and for which the dynamics in the data are expected to follow some physical laws. In this paper, we suggest a multiobjective perspective on the training of PINNs by treating the data loss and the residual loss as two individual objective functions in a truly biobjective optimization approach. As a showcase example, we consider COVID-19 predictions in Germany and built an extended susceptibles-infected-recovered (SIR) model with additionally considered leaky-vaccinated and hospitalized populations (SVIHR model) to model the transition rates and to predict future infections. SIR-type models are expressed by systems of ordinary differential equations (ODEs). We investigate the suitability of the generated PINN for COVID-19 predictions and compare the resulting predicted curves with those obtained by applying the method of non-standard finite differences to the system of ODEs and initial data. The approach is applicable to various systems of ODEs that define dynamical regimes. Those regimes do not need to be SIR-type models, and the corresponding underlying data sets do not have to be associated with COVID-19.

Efficient and Sparse Neural Networks by Pruning Weights in a Multiobjective Learning Approach

Overparameterization and overfitting are common concerns when designing and training deep neural networks, that are often counteracted by pruning and regularization strategies. However, these strategies remain secondary to most learning approaches and suffer from time and computational intensive procedures. We suggest a multiobjective perspective on the training of neural networks by treating its prediction accuracy and the network complexity as two individual objective functions in a biobjective optimization problem. As a showcase example, we use the cross entropy as a measure of the prediction accuracy while adopting an l1-penalty function to assess the total cost (or complexity) of the network parameters. The latter is combined with an intra-training pruning approach that reinforces complexity reduction and requires only marginal extra computational cost. From the perspective of multiobjective optimization, this is a truly large-scale optimization problem. We compare two different optimization paradigms: On the one hand, we adopt a scalarization-based approach that transforms the biobjective problem into a series of weighted-sum scalarizations. On the other hand we implement stochastic multi-gradient descent algorithms that generate a single Pareto optimal solution without requiring or using preference information. In the first case, favorable knee solutions are identified by repeated training runs with adaptively selected scalarization parameters. Preliminary numerical results on exemplary convolutional neural networks confirm that large reductions in the complexity of neural networks with neglibile loss of accuracy are possible.