Anomaly Search Over Many Sequences With Switching Costs

This paper considers the quickest search problem to identify anomalies among large numbers of data streams. These streams can model, for example, disjoint regions monitored by a mobile robot. A particular challenge is a version of the problem in which the experimenter must suffer a cost each time the data stream being sampled changes, such as the time the robot must spend moving between regions. In this paper, we propose an algorithm which accounts for switching costs by varying a confidence threshold that governs when the algorithm switches to a new data stream. Our main contributions are easily computable approximations for both the optimal value of this threshold and the optimal value of the parameter that determines when a stream must be re-sampled. Further, we empirically show (i) a uniform improvement for switching costs of interest and (ii) roughly equivalent performance for small switching costs when comparing to the closest available algorithm.

Differentially Private Controller Synthesis With Metric Temporal Logic Specifications

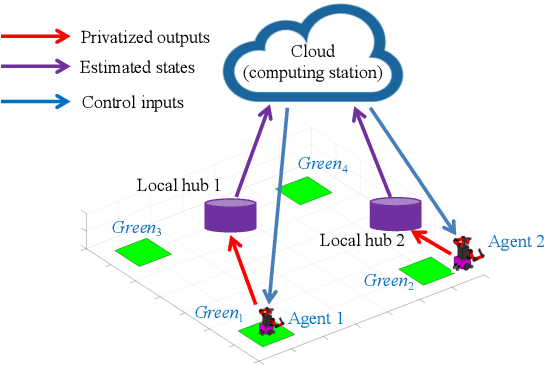
Privacy is an important concern in various multiagent systems in which data collected from the agents are sensitive. We propose a differentially private controller synthesis approach for multi-agent systems subject to high-level specifications expressed in metric temporal logic (MTL). We consider a setting where each agent sends data to a cloud (computing station) through a set of local hubs and the cloud is responsible for computing the control inputs of the agents. Specifically, each agent adds privacy noise (e.g., Gaussian noise) point-wise in time to its own outputs before sharing them with a local hub. Each local hub runs a Kalman filter to estimate the state of the corresponding agent and periodically sends such state estimates to the cloud. The cloud computes the optimal inputs for each agent subject to an MTL specification. While guaranteeing differential privacy of each agent, the controller is also synthesized to ensure a probabilistic guarantee for satisfying the MTL specification.We provide an implementation of the proposed method on a simulation case study with two Baxter-On-Wheels robots as the agents.