Model-adapted Fourier sampling for generative compressed sensing

We study generative compressed sensing when the measurement matrix is randomly subsampled from a unitary matrix (with the DFT as an important special case). It was recently shown that $\textit{O}(kdn\| \boldsymbol{\alpha}\|_{\infty}^{2})$ uniformly random Fourier measurements are sufficient to recover signals in the range of a neural network $G:\mathbb{R}^k \to \mathbb{R}^n$ of depth $d$, where each component of the so-called local coherence vector $\boldsymbol{\alpha}$ quantifies the alignment of a corresponding Fourier vector with the range of $G$. We construct a model-adapted sampling strategy with an improved sample complexity of $\textit{O}(kd\| \boldsymbol{\alpha}\|_{2}^{2})$ measurements. This is enabled by: (1) new theoretical recovery guarantees that we develop for nonuniformly random sampling distributions and then (2) optimizing the sampling distribution to minimize the number of measurements needed for these guarantees. This development offers a sample complexity applicable to natural signal classes, which are often almost maximally coherent with low Fourier frequencies. Finally, we consider a surrogate sampling scheme, and validate its performance in recovery experiments using the CelebA dataset.

A coherence parameter characterizing generative compressed sensing with Fourier measurements

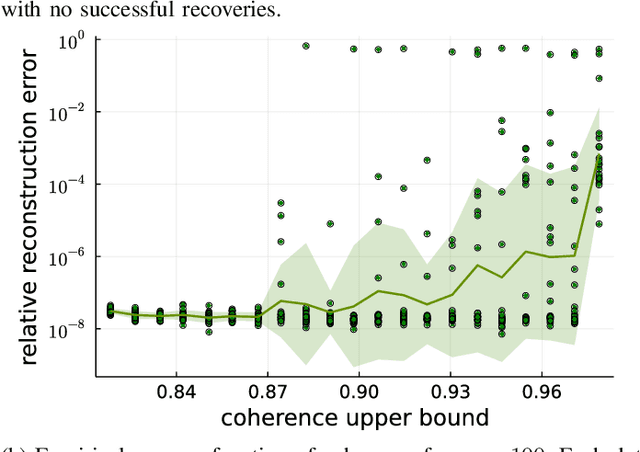
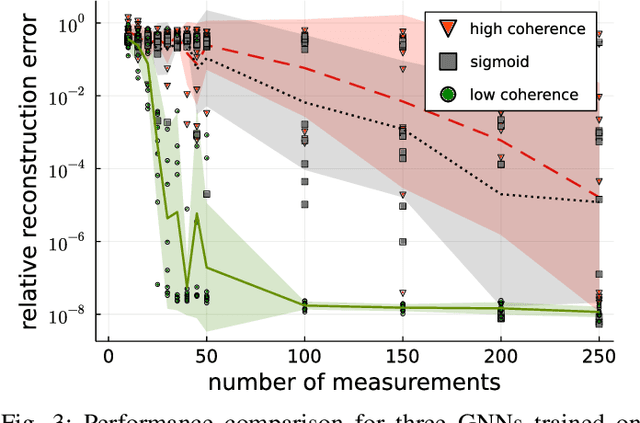
In Bora et al. (2017), a mathematical framework was developed for compressed sensing guarantees in the setting where the measurement matrix is Gaussian and the signal structure is the range of a generative neural network (GNN). The problem of compressed sensing with GNNs has since been extensively analyzed when the measurement matrix and/or network weights follow a subgaussian distribution. We move beyond the subgaussian assumption, to measurement matrices that are derived by sampling uniformly at random rows of a unitary matrix (including subsampled Fourier measurements as a special case). Specifically, we prove the first known restricted isometry guarantee for generative compressed sensing with subsampled isometries, and provide recovery bounds with nearly order-optimal sample complexity, addressing an open problem of Scarlett et al. (2022, p. 10). Recovery efficacy is characterized by the coherence, a new parameter, which measures the interplay between the range of the network and the measurement matrix. Our approach relies on subspace counting arguments and ideas central to high-dimensional probability. Furthermore, we propose a regularization strategy for training GNNs to have favourable coherence with the measurement operator. We provide compelling numerical simulations that support this regularized training strategy: our strategy yields low coherence networks that require fewer measurements for signal recovery. This, together with our theoretical results, supports coherence as a natural quantity for characterizing generative compressed sensing with subsampled isometries.