Matthew J Penn
Leaping through tree space: continuous phylogenetic inference for rooted and unrooted trees
Jun 15, 2023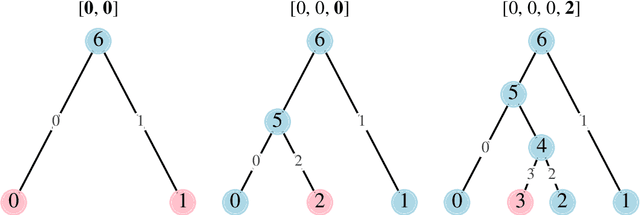
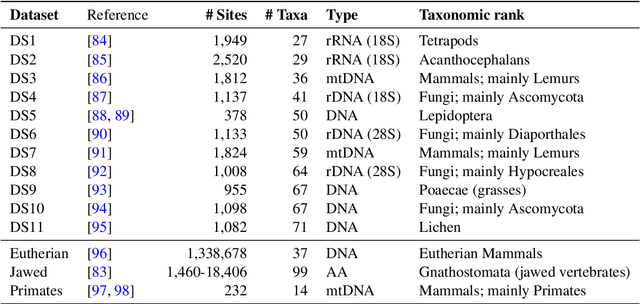
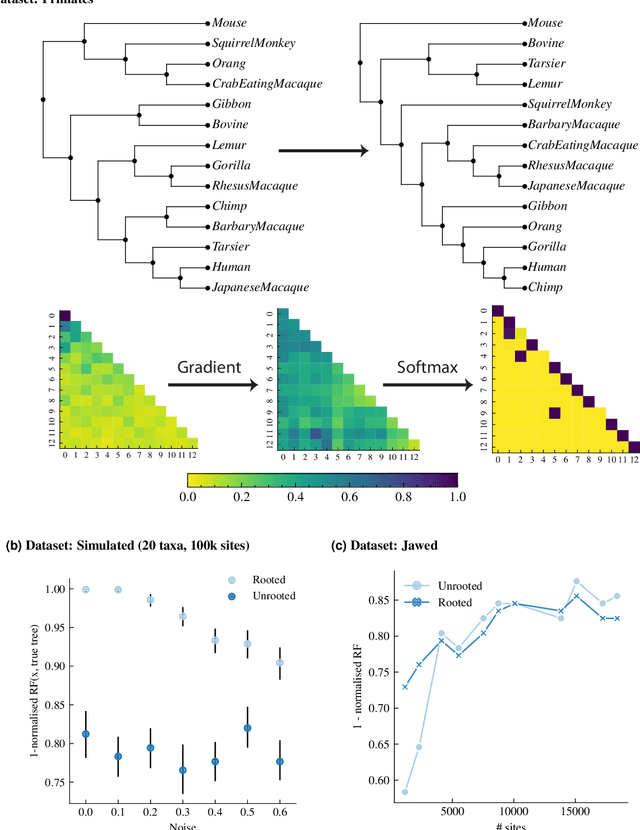
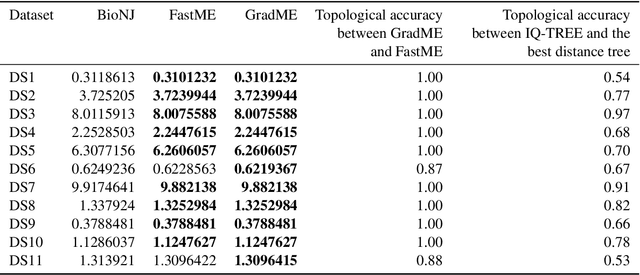
Abstract:Phylogenetics is now fundamental in life sciences, providing insights into the earliest branches of life and the origins and spread of epidemics. However, finding suitable phylogenies from the vast space of possible trees remains challenging. To address this problem, for the first time, we perform both tree exploration and inference in a continuous space where the computation of gradients is possible. This continuous relaxation allows for major leaps across tree space in both rooted and unrooted trees, and is less susceptible to convergence to local minima. Our approach outperforms the current best methods for inference on unrooted trees and, in simulation, accurately infers the tree and root in ultrametric cases. The approach is effective in cases of empirical data with negligible amounts of data, which we demonstrate on the phylogeny of jawed vertebrates. Indeed, only a few genes with an ultrametric signal were generally sufficient for resolving the major lineages of vertebrate. With cubic-time complexity and efficient optimisation via automatic differentiation, our method presents an effective way forwards for exploring the most difficult, data-deficient phylogenetic questions.
Phylo2Vec: a vector representation for binary trees
Apr 25, 2023Abstract:Binary phylogenetic trees inferred from biological data are central to understanding the shared evolutionary history of organisms. Inferring the placement of latent nodes in a tree by any optimality criterion (e.g., maximum likelihood) is an NP-hard problem, propelling the development of myriad heuristic approaches. Yet, these heuristics often lack a systematic means of uniformly sampling random trees or effectively exploring a tree space that grows factorially, which are crucial to optimisation problems such as machine learning. Accordingly, we present Phylo2Vec, a new parsimonious representation of a phylogenetic tree. Phylo2Vec maps any binary tree with $n$ leaves to an integer vector of length $n$. We prove that Phylo2Vec is both well-defined and bijective to the space of phylogenetic trees. The advantages of Phylo2Vec are twofold: i) easy uniform sampling of binary trees and ii) systematic ability to traverse tree space in very large or small jumps. As a proof of concept, we use Phylo2Vec for maximum likelihood inference on five real-world datasets and show that a simple hill climbing-based optimisation efficiently traverses the vastness of tree space from a random to an optimal tree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge