Leaping through tree space: continuous phylogenetic inference for rooted and unrooted trees
Paper and Code
Jun 15, 2023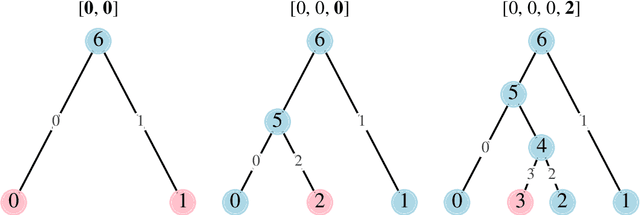
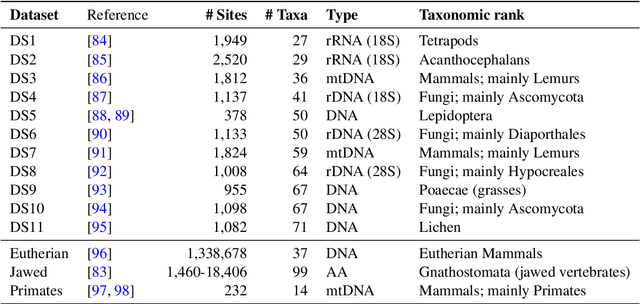
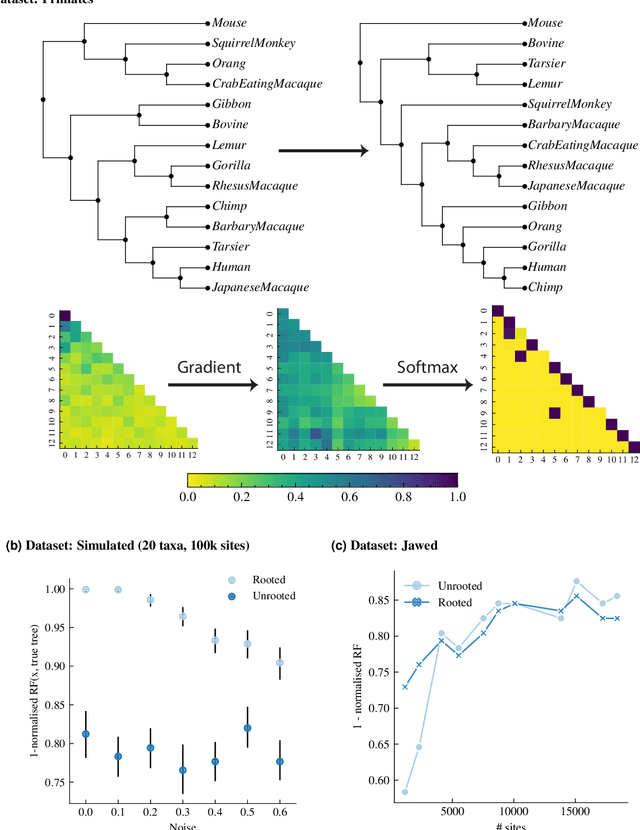
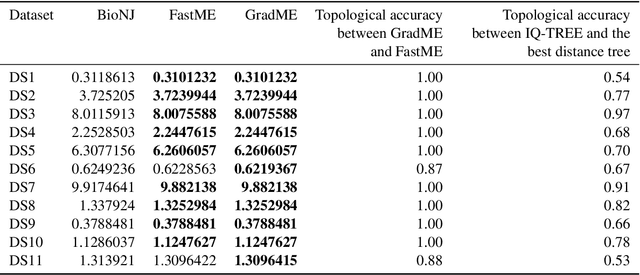
Phylogenetics is now fundamental in life sciences, providing insights into the earliest branches of life and the origins and spread of epidemics. However, finding suitable phylogenies from the vast space of possible trees remains challenging. To address this problem, for the first time, we perform both tree exploration and inference in a continuous space where the computation of gradients is possible. This continuous relaxation allows for major leaps across tree space in both rooted and unrooted trees, and is less susceptible to convergence to local minima. Our approach outperforms the current best methods for inference on unrooted trees and, in simulation, accurately infers the tree and root in ultrametric cases. The approach is effective in cases of empirical data with negligible amounts of data, which we demonstrate on the phylogeny of jawed vertebrates. Indeed, only a few genes with an ultrametric signal were generally sufficient for resolving the major lineages of vertebrate. With cubic-time complexity and efficient optimisation via automatic differentiation, our method presents an effective way forwards for exploring the most difficult, data-deficient phylogenetic questions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge