Matt Baucum
Hidden Markov models are recurrent neural networks: A disease progression modeling application
Jun 04, 2020


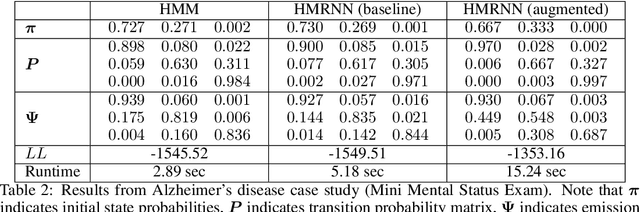
Abstract:Hidden Markov models (HMMs) are commonly used for sequential data modeling when the true state of the system is not fully known. We formulate a special case of recurrent neural networks (RNNs), which we name hidden Markov recurrent neural networks (HMRNNs), and prove that each HMRNN has the same likelihood function as a corresponding discrete-observation HMM. We experimentally validate this theoretical result on synthetic datasets by showing that parameter estimates from HMRNNs are numerically close to those obtained from HMMs via the Baum-Welch algorithm. We demonstrate our method's utility in a case study on Alzheimer's disease progression, in which we augment HMRNNs with other predictive neural networks. The augmented HMRNN yields parameter estimates that offer a novel clinical interpretation and fit the patient data better than HMM parameter estimates from the Baum-Welch algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge