Convex Model Predictive Control for Vehicular Systems

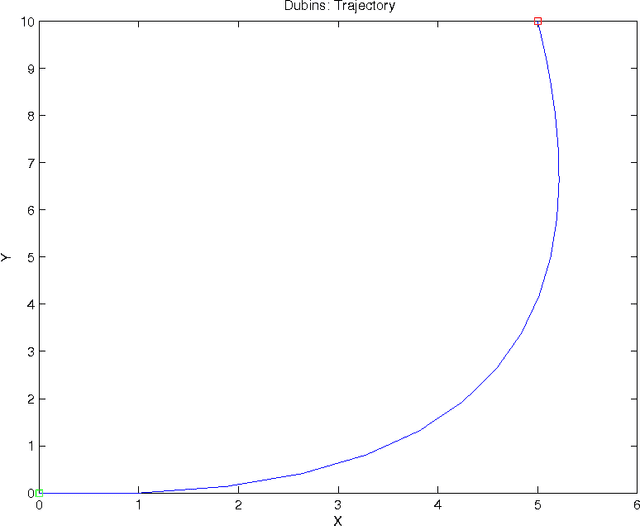
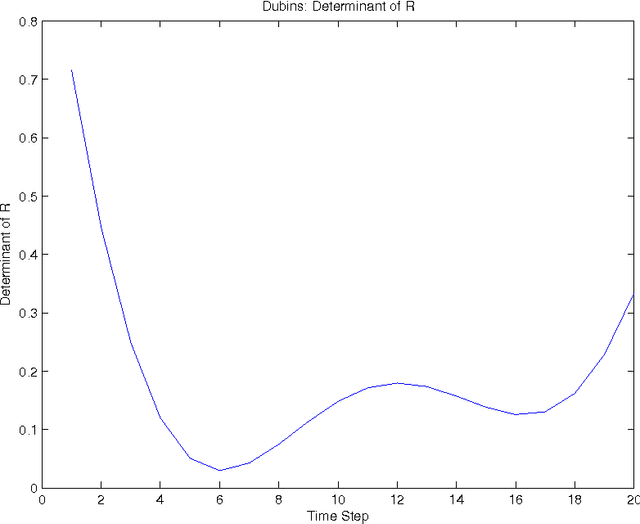
In this work, we present a method to perform Model Predictive Control (MPC) over systems whose state is an element of $SO(n)$ for $n=2,3$. This is done without charts or any local linearization, and instead is performed by operating over the orbitope of rotation matrices. This results in a novel MPC scheme without the drawbacks associated with conventional linearization techniques. Instead, second order cone- or semidefinite-constraints on state variables are the only requirement beyond those of a QP-scheme typical for MPC of linear systems. Of particular emphasis is the application to aeronautical and vehicular systems, wherein the method removes many of the transcendental trigonometric terms associated with these systems' state space equations. Furthermore, the method is shown to be compatible with many existing variants of MPC, including obstacle avoidance via Mixed Integer Linear Programming (MILP).

Optimal Navigation Functions for Nonlinear Stochastic Systems

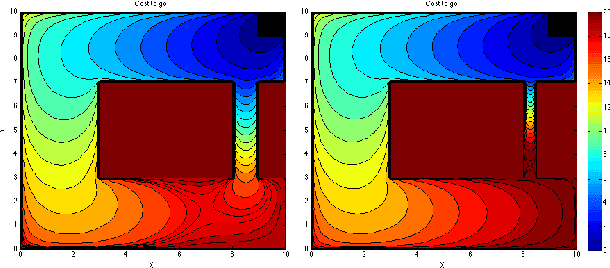
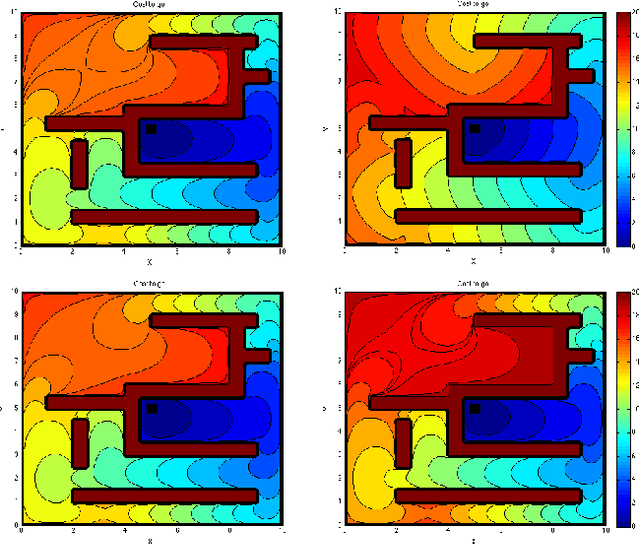
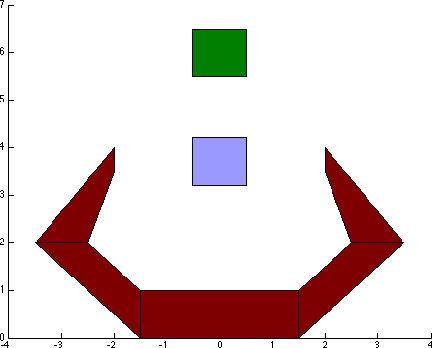
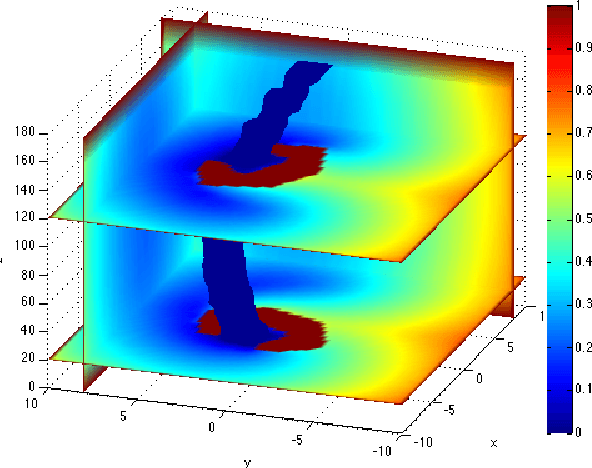
This paper presents a new methodology to craft navigation functions for nonlinear systems with stochastic uncertainty. The method relies on the transformation of the Hamilton-Jacobi-Bellman (HJB) equation into a linear partial differential equation. This approach allows for optimality criteria to be incorporated into the navigation function, and generalizes several existing results in navigation functions. It is shown that the HJB and that existing navigation functions in the literature sit on ends of a spectrum of optimization problems, upon which tradeoffs may be made in problem complexity. In particular, it is shown that under certain criteria the optimal navigation function is related to Laplace's equation, previously used in the literature, through an exponential transform. Further, analytical solutions to the HJB are available in simplified domains, yielding guidance towards optimality for approximation schemes. Examples are used to illustrate the role that noise, and optimality can potentially play in navigation system design.

Convex Relaxations of SE and SE for Visual Pose Estimation

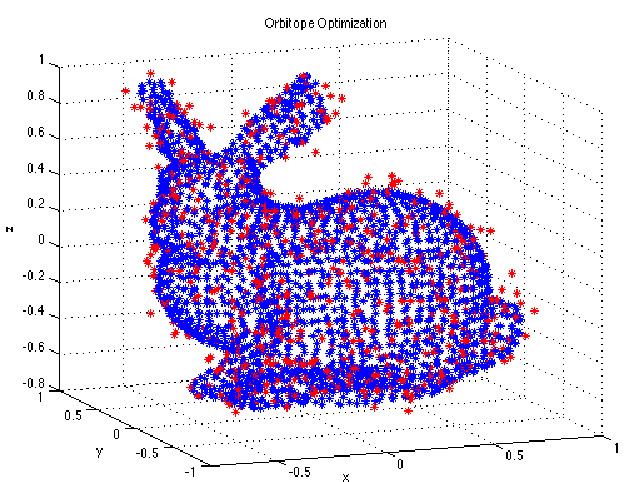
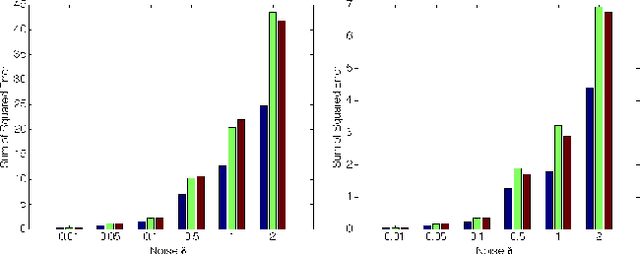
This paper proposes a new method for rigid body pose estimation based on spectrahedral representations of the tautological orbitopes of $SE(2)$ and $SE(3)$. The approach can use dense point cloud data from stereo vision or an RGB-D sensor (such as the Microsoft Kinect), as well as visual appearance data. The method is a convex relaxation of the classical pose estimation problem, and is based on explicit linear matrix inequality (LMI) representations for the convex hulls of $SE(2)$ and $SE(3)$. Given these representations, the relaxed pose estimation problem can be framed as a robust least squares problem with the optimization variable constrained to these convex sets. Although this formulation is a relaxation of the original problem, numerical experiments indicate that it is indeed exact - i.e. its solution is a member of $SE(2)$ or $SE(3)$ - in many interesting settings. We additionally show that this method is guaranteed to be exact for a large class of pose estimation problems.