Category Theoretic Analysis of Photon-based Decision Making

Decision making is a vital function in this age of machine learning and artificial intelligence, yet its physical realization and theoretical fundamentals are still not completely understood. In our former study, we demonstrated that single-photons can be used to make decisions in uncertain, dynamically changing environments. The two-armed bandit problem was successfully solved using the dual probabilistic and particle attributes of single photons. In this study, we present a category theoretic modeling and analysis of single-photon-based decision making, including a quantitative analysis that is in agreement with the experimental results. A category theoretic model reveals the complex interdependencies of subject matter entities in a simplified manner, even in dynamically changing environments. In particular, the octahedral and braid structures in triangulated categories provide a better understanding and quantitative metrics of the underlying mechanisms of a single-photon decision maker. This study provides both insight and a foundation for analyzing more complex and uncertain problems, to further machine learning and artificial intelligence.

Harnessing Natural Fluctuations: Analogue Computer for Efficient Socially Maximal Decision Making

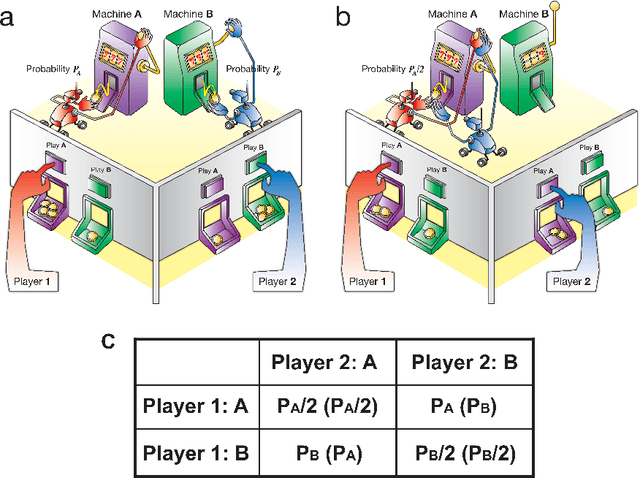
Each individual handles many tasks of finding the most profitable option from a set of options that stochastically provide rewards. Our society comprises a collection of such individuals, and the society is expected to maximise the total rewards, while the individuals compete for common rewards. Such collective decision making is formulated as the `competitive multi-armed bandit problem (CBP)', requiring a huge computational cost. Herein, we demonstrate a prototype of an analog computer that efficiently solves CBPs by exploiting the physical dynamics of numerous fluids in coupled cylinders. This device enables the maximisation of the total rewards for the society without paying the conventionally required computational cost; this is because the fluids estimate the reward probabilities of the options for the exploitation of past knowledge and generate random fluctuations for the exploration of new knowledge. Our results suggest that to optimise the social rewards, the utilisation of fluid-derived natural fluctuations is more advantageous than applying artificial external fluctuations. Our analog computing scheme is expected to trigger further studies for harnessing the huge computational power of natural phenomena for resolving a wide variety of complex problems in modern information society.

Decision Maker using Coupled Incompressible-Fluid Cylinders

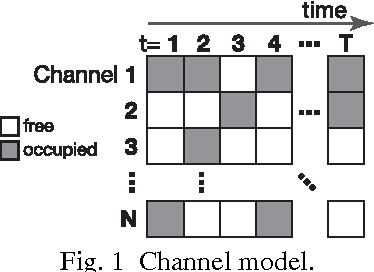
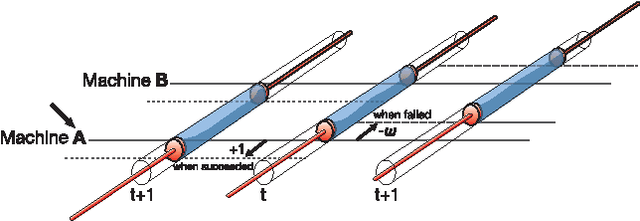
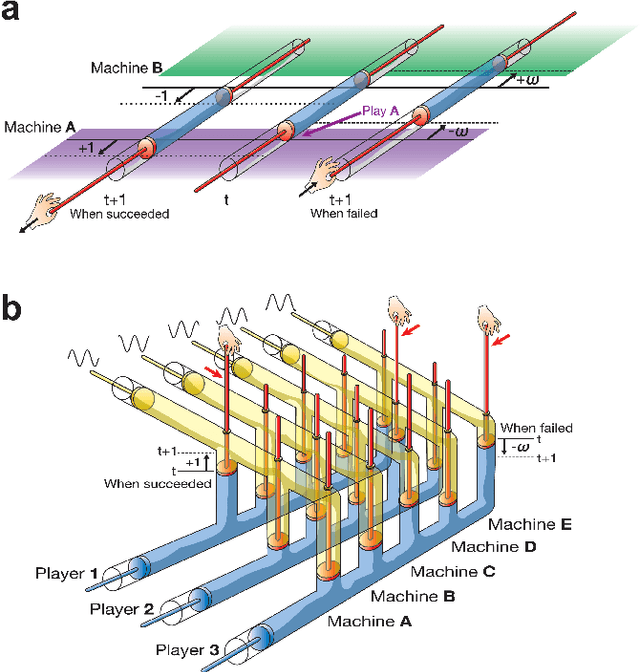
The multi-armed bandit problem (MBP) is the problem of finding, as accurately and quickly as possible, the most profitable option from a set of options that gives stochastic rewards by referring to past experiences. Inspired by fluctuated movements of a rigid body in a tug-of-war game, we formulated a unique search algorithm that we call the `tug-of-war (TOW) dynamics' for solving the MBP efficiently. The cognitive medium access, which refers to multi-user channel allocations in cognitive radio, can be interpreted as the competitive multi-armed bandit problem (CMBP); the problem is to determine the optimal strategy for allocating channels to users which yields maximum total rewards gained by all users. Here we show that it is possible to construct a physical device for solving the CMBP, which we call the `TOW Bombe', by exploiting the TOW dynamics existed in coupled incompressible-fluid cylinders. This analog computing device achieves the `socially-maximum' resource allocation that maximizes the total rewards in cognitive medium access without paying a huge computational cost that grows exponentially as a function of the problem size.

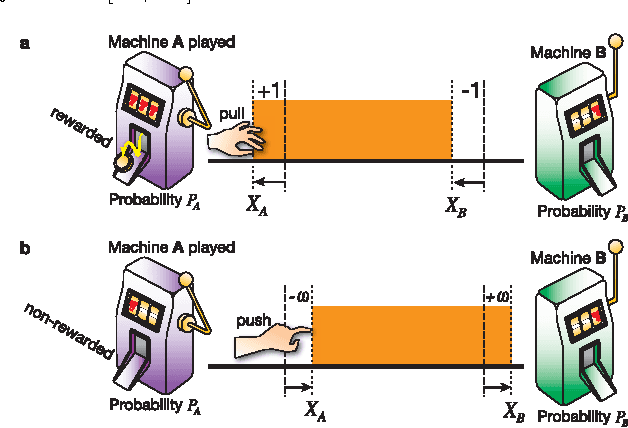
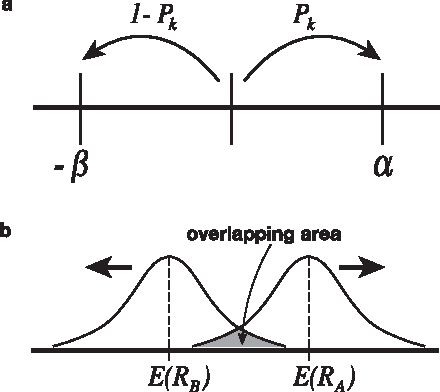
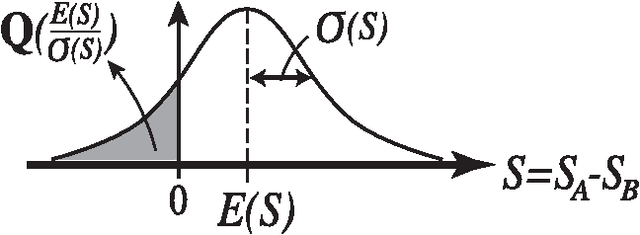
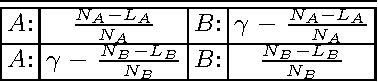
Efficient Decision-Making by Volume-Conserving Physical Object

We demonstrate that any physical object, as long as its volume is conserved when coupled with suitable operations, provides a sophisticated decision-making capability. We consider the problem of finding, as accurately and quickly as possible, the most profitable option from a set of options that gives stochastic rewards. These decisions are made as dictated by a physical object, which is moved in a manner similar to the fluctuations of a rigid body in a tug-of-war game. Our analytical calculations validate statistical reasons why our method exhibits higher efficiency than conventional algorithms.