Calibrating the Predictions for Top-N Recommendations

Well-calibrated predictions of user preferences are essential for many applications. Since recommender systems typically select the top-N items for users, calibration for those top-N items, rather than for all items, is important. We show that previous calibration methods result in miscalibrated predictions for the top-N items, despite their excellent calibration performance when evaluated on all items. In this work, we address the miscalibration in the top-N recommended items. We first define evaluation metrics for this objective and then propose a generic method to optimize calibration models focusing on the top-N items. It groups the top-N items by their ranks and optimizes distinct calibration models for each group with rank-dependent training weights. We verify the effectiveness of the proposed method for both explicit and implicit feedback datasets, using diverse classes of recommender models.

Online Evaluation Methods for the Causal Effect of Recommendations

Evaluating the causal effect of recommendations is an important objective because the causal effect on user interactions can directly leads to an increase in sales and user engagement. To select an optimal recommendation model, it is common to conduct A/B testing to compare model performance. However, A/B testing of causal effects requires a large number of users, making such experiments costly and risky. We therefore propose the first interleaving methods that can efficiently compare recommendation models in terms of causal effects. In contrast to conventional interleaving methods, we measure the outcomes of both items on an interleaved list and items not on the interleaved list, since the causal effect is the difference between outcomes with and without recommendations. To ensure that the evaluations are unbiased, we either select items with equal probability or weight the outcomes using inverse propensity scores. We then verify the unbiasedness and efficiency of online evaluation methods through simulated online experiments. The results indicate that our proposed methods are unbiased and that they have superior efficiency to A/B testing.

Causality-Aware Neighborhood Methods for Recommender Systems

The business objectives of recommenders, such as increasing sales, are aligned with the causal effect of recommendations. Previous recommenders targeting for the causal effect employ the inverse propensity scoring (IPS) in causal inference. However, IPS is prone to suffer from high variance. The matching estimator is another representative method in causal inference field. It does not use propensity and hence free from the above variance problem. In this work, we unify traditional neighborhood recommendation methods with the matching estimator, and develop robust ranking methods for the causal effect of recommendations. Our experiments demonstrate that the proposed methods outperform various baselines in ranking metrics for the causal effect. The results suggest that the proposed methods can achieve more sales and user engagement than previous recommenders.

Approximation Methods for Kernelized Bandits

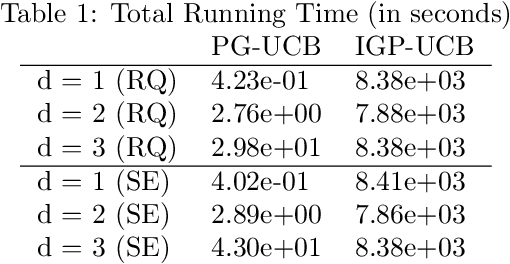
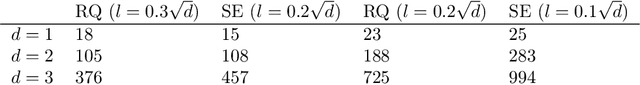
The RKHS bandit problem (also called kernelized multi-armed bandit problem) is an online optimization problem of non-linear functions with noisy feedbacks. Most of the existing methods for the problem have sub-linear regret guarantee at the cost of high computational complexity. For example, IGP-UCB requires at least quadratic time in the number of observed samples at each round. In this paper, using deep results provided by the approximation theory, we approximately reduce the problem to the well-studied linear bandit problem of an appropriate dimension. Then, we propose several algorithms and prove that they achieve comparable regret guarantee to the existing methods (GP-UCB, IGP-UCB) with less computational complexity. Specifically, our proposed methods require polylogarithmic time to select an arm at each round for kernels with "infinite smoothness" (e.g. the rational quadratic and squared exponential kernels). Furthermore, we empirically show our proposed method has comparable regret to the existing method and its running time is much shorter.

Unbiased Learning for the Causal Effect of Recommendation

Increasing users' positive interactions, such as purchases or clicks, is an important objective of recommender systems. Recommenders typically aim to select items that users will interact with. If the recommended items are purchased, an increase in sales is expected. However, the items could have been purchased even without recommendation. Thus, we want to recommend items that results in purchases caused by recommendation. This can be formulated as a ranking problem in terms of the causal effect. Despite its importance, this problem has not been well explored in the related research. It is challenging because the ground truth of causal effect is unobservable, and estimating the causal effect is prone to the bias arising from currently deployed recommenders. This paper proposes an unbiased learning framework for the causal effect of recommendation. Based on the inverse propensity scoring technique, the proposed framework first constructs unbiased estimators for ranking metrics. Then, it conducts empirical risk minimization on the estimators with propensity capping, which reduces variance under finite training samples. Based on the framework, we develop an unbiased learning method for the causal effect extension of a ranking metric. We theoretically analyze the unbiasedness of the proposed method and empirically demonstrate that the proposed method outperforms other biased learning methods in various settings.

Submodular Bandit Problem Under Multiple Constraints

The linear submodular bandit problem was proposed to simultaneously address diversified retrieval and online learning in a recommender system. If there is no uncertainty, this problem is equivalent to a submodular maximization problem under a cardinality constraint. However, in some situations, recommendation lists should satisfy additional constraints such as budget constraints, other than a cardinality constraint. Thus, motivated by diversified retrieval considering budget constraints, we introduce a submodular bandit problem under the intersection of $l$ knapsacks and a $k$-system constraint. Here $k$-system constraints form a very general class of constraints including cardinality constraints and the intersection of $k$ matroid constraints. To solve this problem, we propose a non-greedy algorithm that adaptively focuses on a standard or modified upper-confidence bound. We provide a high-probability upper bound of an approximation regret, where the approximation ratio matches that of a fast offline algorithm. Moreover, we perform experiments under various combinations of constraints using a synthetic and two real-world datasets and demonstrate that our proposed methods outperform the existing baselines.