A Bayesian take on option pricing with Gaussian processes

Local volatility is a versatile option pricing model due to its state dependent diffusion coefficient. Calibration is, however, non-trivial as it involves both proposing a hypothesis model of the latent function and a method for fitting it to data. In this paper we present novel Bayesian inference with Gaussian process priors. We obtain a rich representation of the local volatility function with a probabilistic notion of uncertainty attached to the calibrate. We propose an inference algorithm and apply our approach to S&P 500 market data.

Sequential sampling of Gaussian process latent variable models

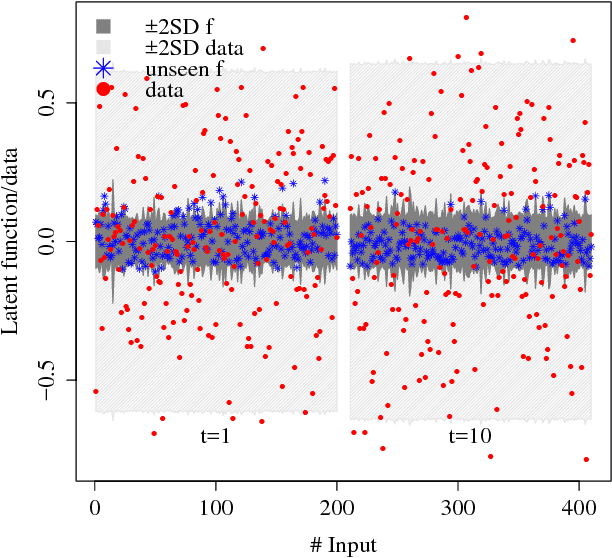
We consider the problem of inferring a latent function in a probabilistic model of data. When dependencies of the latent function are specified by a Gaussian process and the data likelihood is complex, efficient computation often involve Markov chain Monte Carlo sampling with limited applicability to large data sets. We extend some of these techniques to scale efficiently when the problem exhibits a sequential structure. We propose an approximation that enables sequential sampling of both latent variables and associated parameters. We demonstrate strong performance in growing-data settings that would otherwise be unfeasible with naive, non-sequential sampling.