Sequential sampling of Gaussian process latent variable models
Paper and Code
Jul 20, 2018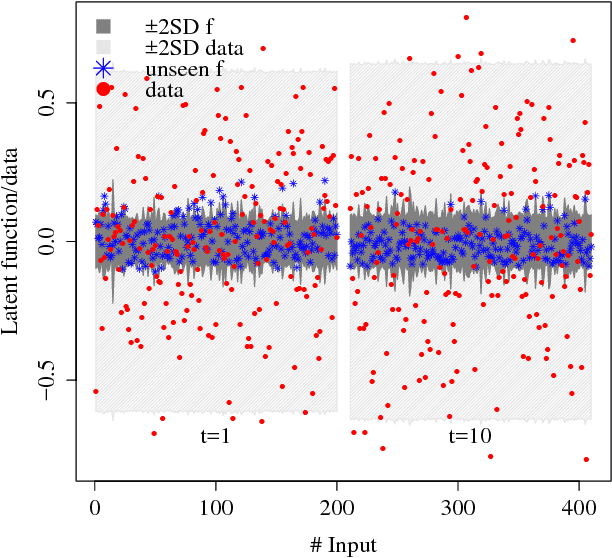



We consider the problem of inferring a latent function in a probabilistic model of data. When dependencies of the latent function are specified by a Gaussian process and the data likelihood is complex, efficient computation often involve Markov chain Monte Carlo sampling with limited applicability to large data sets. We extend some of these techniques to scale efficiently when the problem exhibits a sequential structure. We propose an approximation that enables sequential sampling of both latent variables and associated parameters. We demonstrate strong performance in growing-data settings that would otherwise be unfeasible with naive, non-sequential sampling.
* In 2018 ICML Workshop on Tractable Probabilistic Models (TPM 2018)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge