Comparative Analysis of Predicting Subsequent Steps in Hénon Map

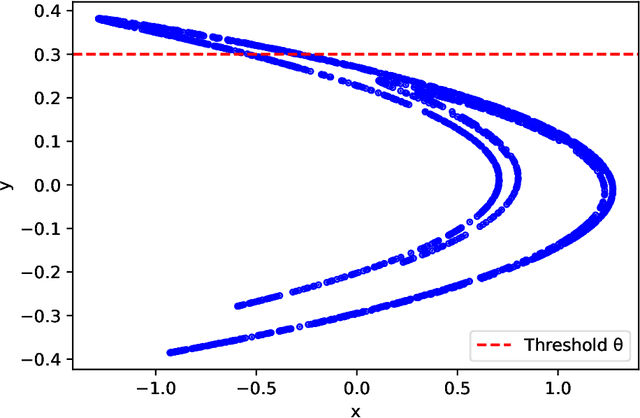
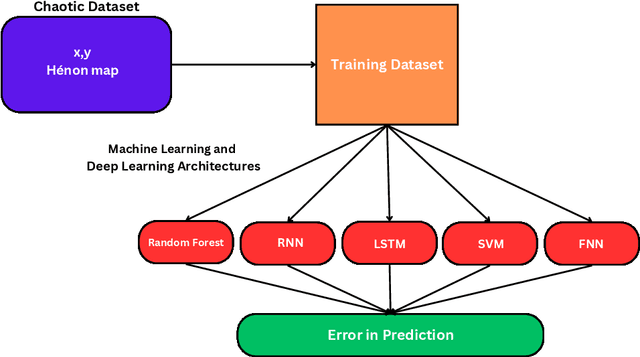
This paper explores the prediction of subsequent steps in H\'enon Map using various machine learning techniques. The H\'enon map, well known for its chaotic behaviour, finds applications in various fields including cryptography, image encryption, and pattern recognition. Machine learning methods, particularly deep learning, are increasingly essential for understanding and predicting chaotic phenomena. This study evaluates the performance of different machine learning models including Random Forest, Recurrent Neural Network (RNN), Long Short-Term Memory (LSTM) networks, Support Vector Machines (SVM), and Feed Forward Neural Networks (FNN) in predicting the evolution of the H\'enon map. Results indicate that LSTM network demonstrate superior predictive accuracy, particularly in extreme event prediction. Furthermore, a comparison between LSTM and FNN models reveals the LSTM's advantage, especially for longer prediction horizons and larger datasets. This research underscores the significance of machine learning in elucidating chaotic dynamics and highlights the importance of model selection and dataset size in forecasting subsequent steps in chaotic systems.

Explaining wall-bounded turbulence through deep learning

Despite its great scientific and technological importance, wall-bounded turbulence is an unresolved problem that requires new perspectives to be tackled. One of the key strategies has been to study interactions among the coherent structures in the flow. Such interactions are explored in this study for the first time using an explainable deep-learning method. The instantaneous velocity field in a turbulent channel is used to predict the velocity field in time through a convolutional neural network. The predicted flow is used to assess the importance of each structure for this prediction using a game-theoretic algorithm (SHapley Additive exPlanations). This work provides results in agreement with previous observations in the literature and extends them by quantifying the importance of the Reynolds-stress structures, finding a causal connection between these structures and the dynamics of the flow. The process, based on deep-learning explainability, has the potential to shed light on numerous fundamental phenomena of wall-bounded turbulence, including the objective definition of new types of flow structures.

Using Machine Learning to predict extreme events in the Hénon map

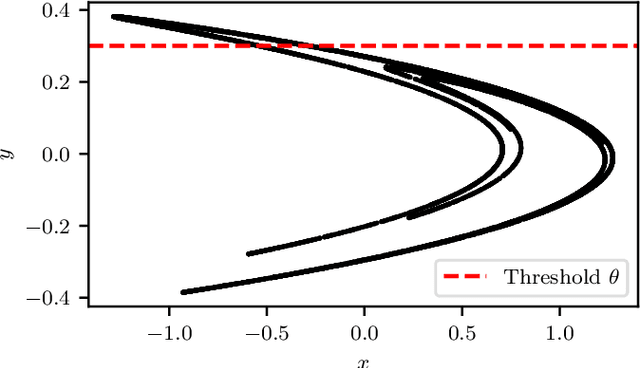
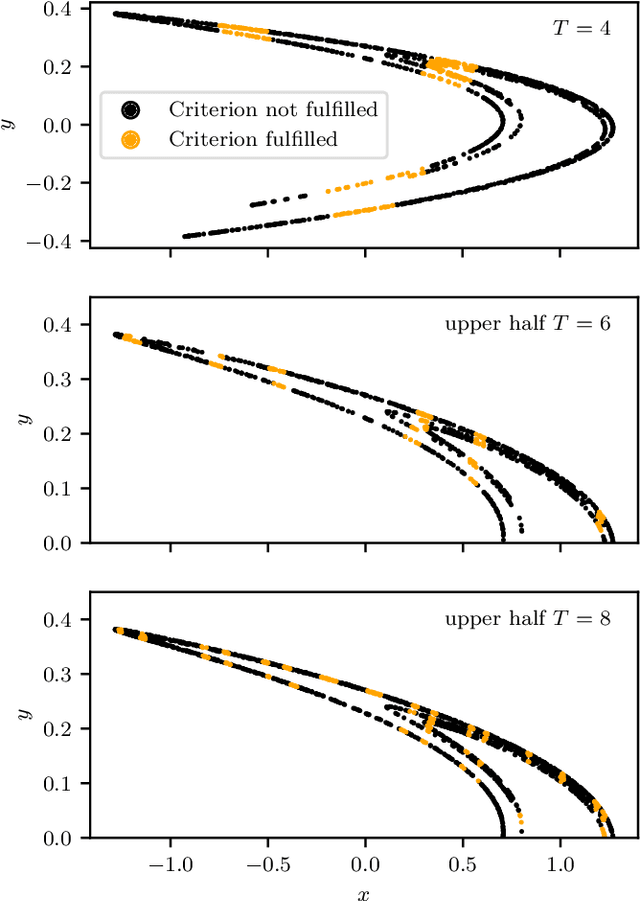
Machine Learning (ML) inspired algorithms provide a flexible set of tools for analyzing and forecasting chaotic dynamical systems. We here analyze the performance of one algorithm for the prediction of extreme events in the two-dimensional H\'enon map at the classical parameters. The task is to determine whether a trajectory will exceed a threshold after a set number of time steps into the future. This task has a geometric interpretation within the dynamics of the H\'enon map, which we use to gauge the performance of the neural networks that are used in this work. We analyze the dependence of the success rate of the ML models on the prediction time $T$ , the number of training samples $N_T$ and the size of the network $N_p$. We observe that in order to maintain a certain accuracy, $N_T \propto exp(2 h T)$ and $N_p \propto exp(hT)$, where $h$ is the topological entropy. Similar relations between the intrinsic chaotic properties of the dynamics and ML parameters might be observable in other systems as well.