Using Machine Learning to predict extreme events in the Hénon map
Paper and Code
Feb 20, 2020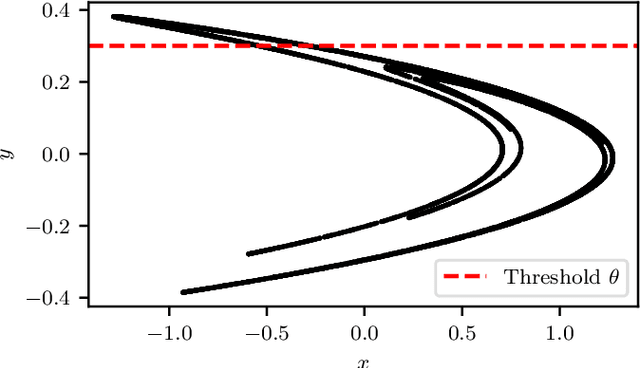
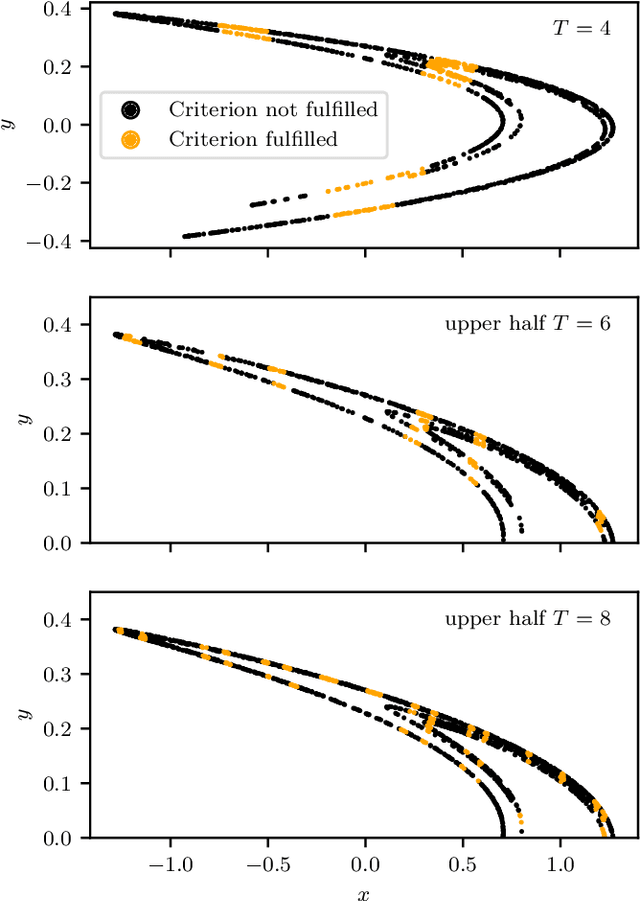


Machine Learning (ML) inspired algorithms provide a flexible set of tools for analyzing and forecasting chaotic dynamical systems. We here analyze the performance of one algorithm for the prediction of extreme events in the two-dimensional H\'enon map at the classical parameters. The task is to determine whether a trajectory will exceed a threshold after a set number of time steps into the future. This task has a geometric interpretation within the dynamics of the H\'enon map, which we use to gauge the performance of the neural networks that are used in this work. We analyze the dependence of the success rate of the ML models on the prediction time $T$ , the number of training samples $N_T$ and the size of the network $N_p$. We observe that in order to maintain a certain accuracy, $N_T \propto exp(2 h T)$ and $N_p \propto exp(hT)$, where $h$ is the topological entropy. Similar relations between the intrinsic chaotic properties of the dynamics and ML parameters might be observable in other systems as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge