Markus Nissl
Complexity of Arithmetic in Warded Datalog+-
Feb 10, 2022Abstract:Warded Datalog+- extends the logic-based language Datalog with existential quantifiers in rule heads. Existential rules are needed for advanced reasoning tasks, e.g., ontological reasoning. The theoretical efficiency guarantees of Warded Datalog+- do not cover extensions crucial for data analytics, such as arithmetic. Moreover, despite the significance of arithmetic for common data analytic scenarios, no decidable fragment of any Datalog+- language extended with arithmetic has been identified. We close this gap by defining a new language that extends Warded Datalog+- with arithmetic and prove its P-completeness. Furthermore, we present an efficient reasoning algorithm for our newly defined language and prove descriptive complexity results for a recently introduced Datalog fragment with integer arithmetic, thereby closing an open question. We lay the theoretical foundation for highly expressive Datalog+- languages that combine the power of advanced recursive rules and arithmetic while guaranteeing efficient reasoning algorithms for applications in modern AI systems, such as Knowledge Graphs.
Query Evaluation in DatalogMTL -- Taming Infinite Query Results
Sep 21, 2021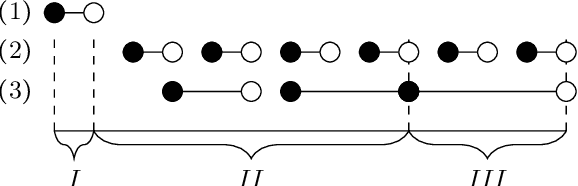
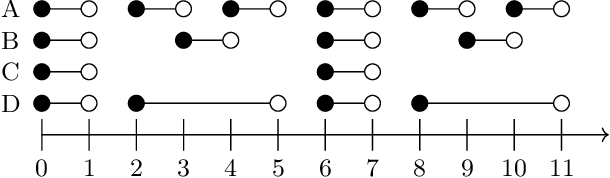
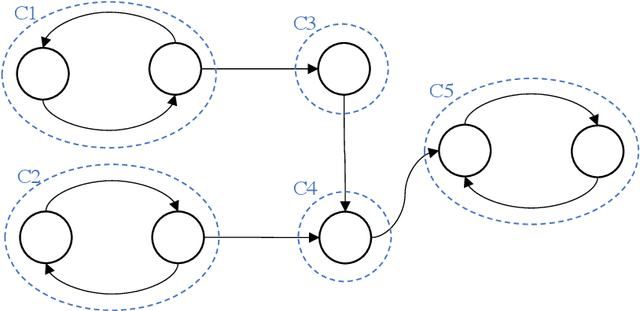
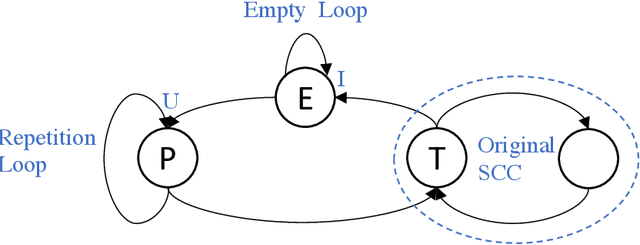
Abstract:In this paper, we investigate finite representations of DatalogMTL. First, we introduce programs that have finite models and propose a toolkit for structuring the execution of DatalogMTL rules into sequential phases. Then, we study infinite models that eventually become constant and introduce sufficient criteria for programs that allow for such representation. We proceed by considering infinite models that are eventually periodic and show that such a representation encompasses all DatalogMTLFP programs, a widely discussed fragment. Finally, we provide a novel algorithm for reasoning over finite representable DatalogMTL programs that incorporates all of the previously discussed representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge