Mark Tuddenham
Orthogonalising gradients to speed up neural network optimisation
Feb 14, 2022
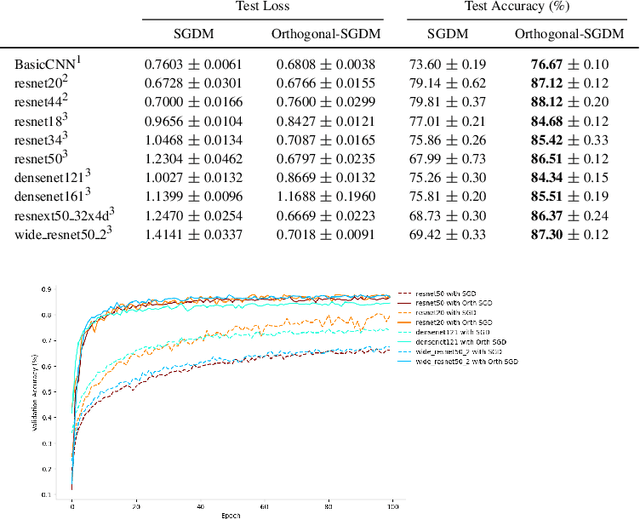
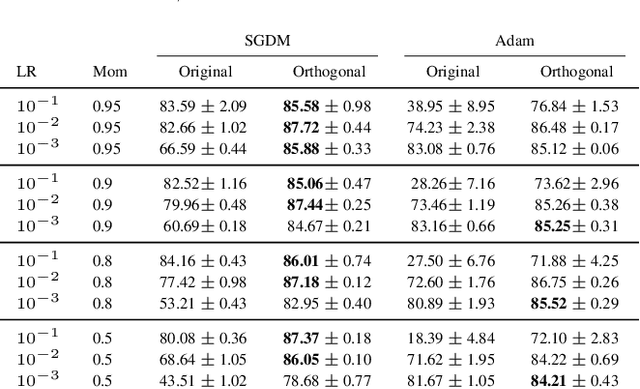

Abstract:The optimisation of neural networks can be sped up by orthogonalising the gradients before the optimisation step, ensuring the diversification of the learned representations. We orthogonalise the gradients of the layer's components/filters with respect to each other to separate out the intermediate representations. Our method of orthogonalisation allows the weights to be used more flexibly, in contrast to restricting the weights to an orthogonalised sub-space. We tested this method on ImageNet and CIFAR-10 resulting in a large decrease in learning time, and also obtain a speed-up on the semi-supervised learning BarlowTwins. We obtain similar accuracy to SGD without fine-tuning and better accuracy for na\"ively chosen hyper-parameters.
Quasi-Newton's method in the class gradient defined high-curvature subspace
Nov 28, 2020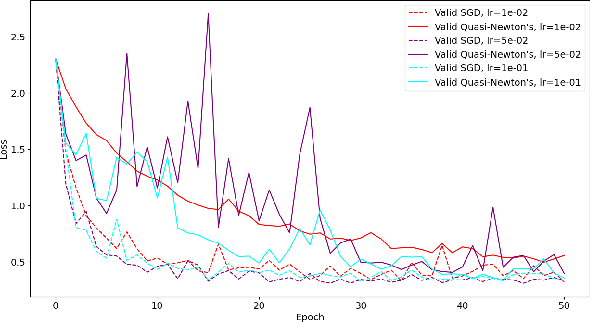
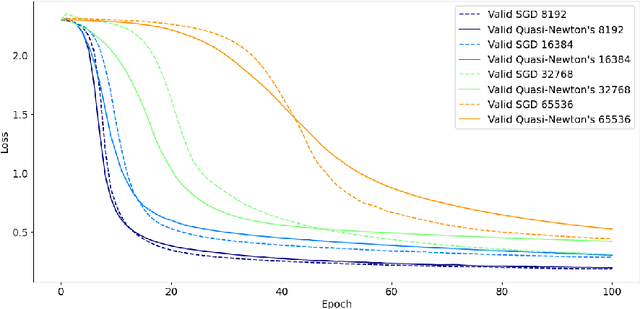
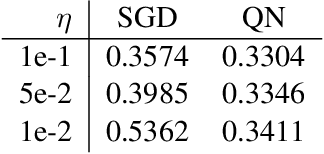
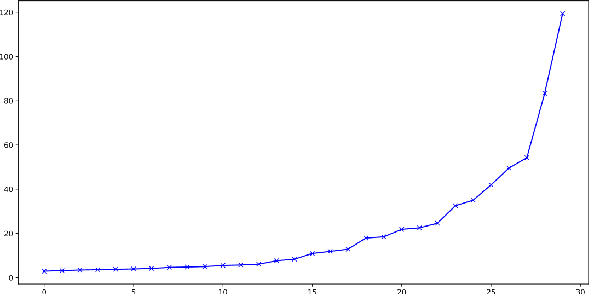
Abstract:Classification problems using deep learning have been shown to have a high-curvature subspace in the loss landscape equal in dimension to the number of classes. Moreover, this subspace corresponds to the subspace spanned by the logit gradients for each class. An obvious strategy to speed up optimisation would be to use Newton's method in the high-curvature subspace and stochastic gradient descent in the co-space. We show that a naive implementation actually slows down convergence and we speculate why this might be.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge