Constrained Training of Neural Networks via Theorem Proving

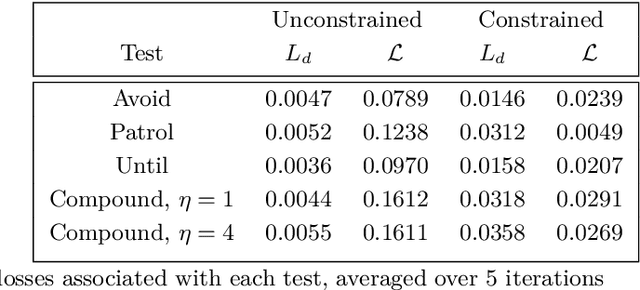
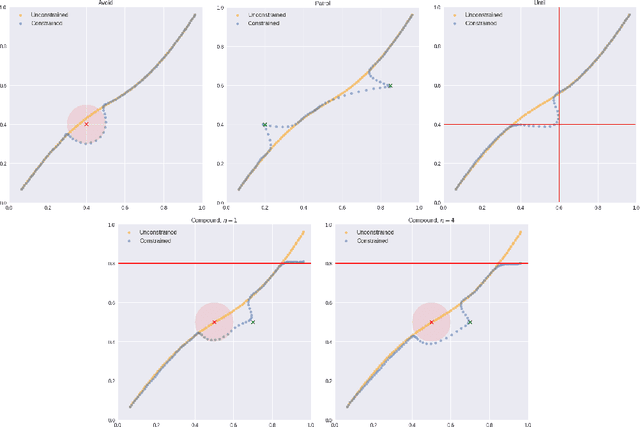
We introduce a theorem proving approach to the specification and generation of temporal logical constraints for training neural networks. We formalise a deep embedding of linear temporal logic over finite traces (LTL$_f$) and an associated evaluation function characterising its semantics within the higher-order logic of the Isabelle theorem prover. We then proceed to formalise a loss function $\mathcal{L}$ that we formally prove to be sound, and differentiable to a function $d\mathcal{L}$. We subsequently use Isabelle's automatic code generation mechanism to produce OCaml versions of LTL$_f$, $\mathcal{L}$ and $d\mathcal{L}$ that we integrate with PyTorch via OCaml bindings for Python. We show that, when used for training in an existing deep learning framework for dynamic movement, our approach produces expected results for common movement specification patterns such as obstacle avoidance and patrolling. The distinctive benefit of our approach is the fully rigorous method for constrained training, eliminating many of the risks inherent to ad-hoc implementations of logical aspects directly in an "unsafe" programming language such as Python.

Formalising the Foundations of Discrete Reinforcement Learning in Isabelle/HOL

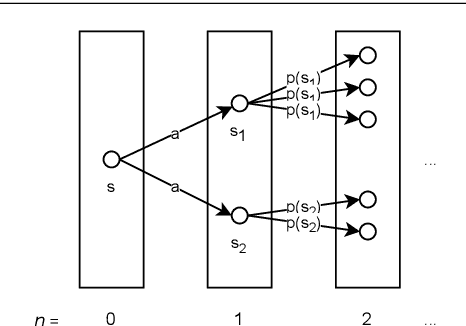
We present a formalisation of finite Markov decision processes with rewards in the Isabelle theorem prover. We focus on the foundations required for dynamic programming and the use of reinforcement learning agents over such processes. In particular, we derive the Bellman equation from first principles (in both scalar and vector form), derive a vector calculation that produces the expected value of any policy p, and go on to prove the existence of a universally optimal policy where there is a discounting factor less than one. Lastly, we prove that the value iteration and the policy iteration algorithms work in finite time, producing an epsilon-optimal and a fully optimal policy respectively.