Formalising the Foundations of Discrete Reinforcement Learning in Isabelle/HOL
Paper and Code
Dec 11, 2021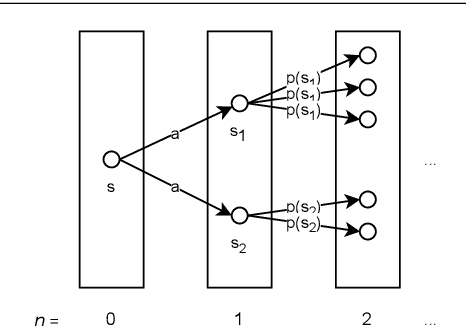
We present a formalisation of finite Markov decision processes with rewards in the Isabelle theorem prover. We focus on the foundations required for dynamic programming and the use of reinforcement learning agents over such processes. In particular, we derive the Bellman equation from first principles (in both scalar and vector form), derive a vector calculation that produces the expected value of any policy p, and go on to prove the existence of a universally optimal policy where there is a discounting factor less than one. Lastly, we prove that the value iteration and the policy iteration algorithms work in finite time, producing an epsilon-optimal and a fully optimal policy respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge