The Credibility Transformer

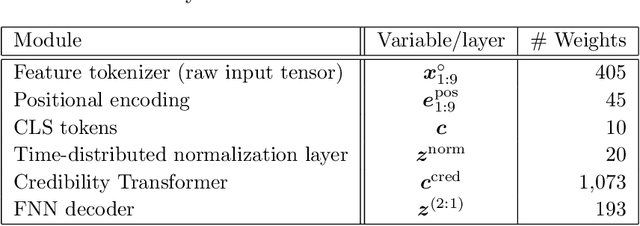
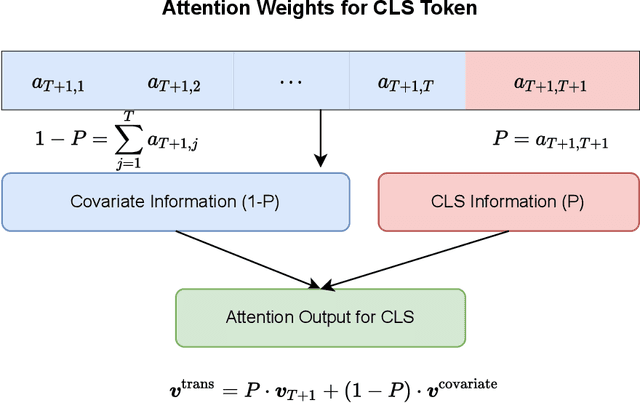
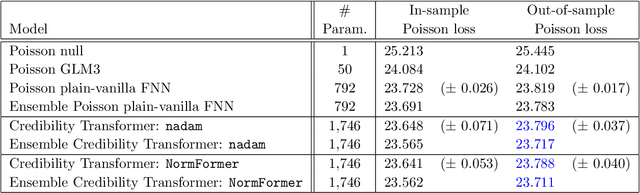
Inspired by the large success of Transformers in Large Language Models, these architectures are increasingly applied to tabular data. This is achieved by embedding tabular data into low-dimensional Euclidean spaces resulting in similar structures as time-series data. We introduce a novel credibility mechanism to this Transformer architecture. This credibility mechanism is based on a special token that should be seen as an encoder that consists of a credibility weighted average of prior information and observation based information. We demonstrate that this novel credibility mechanism is very beneficial to stabilize training, and our Credibility Transformer leads to predictive models that are superior to state-of-the-art deep learning models.

Conditional expectation network for SHAP

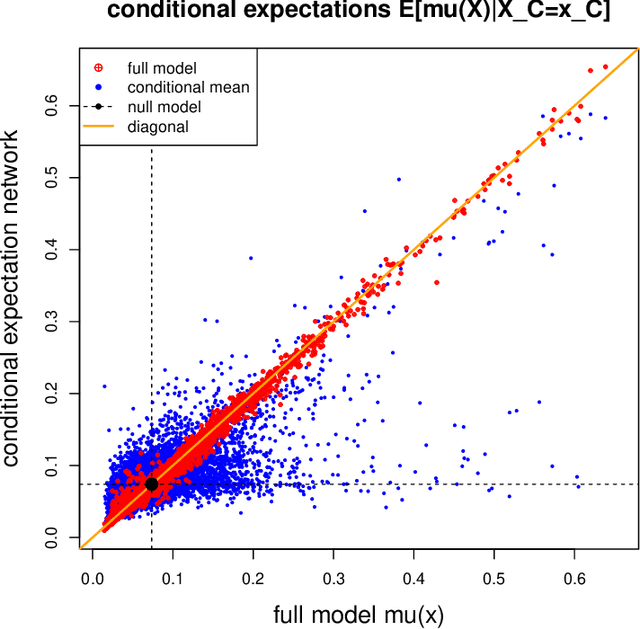
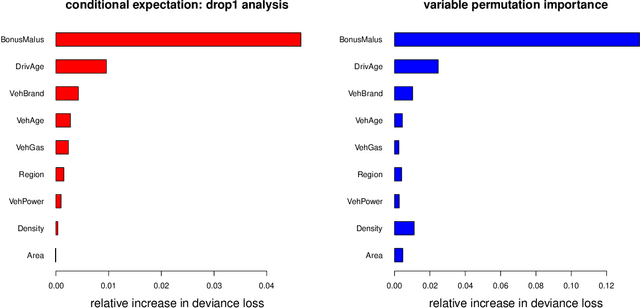
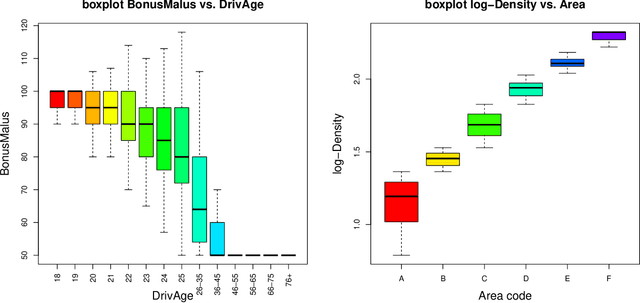
A very popular model-agnostic technique for explaining predictive models is the SHapley Additive exPlanation (SHAP). The two most popular versions of SHAP are a conditional expectation version and an unconditional expectation version (the latter is also known as interventional SHAP). Except for tree-based methods, usually the unconditional version is used (for computational reasons). We provide a (surrogate) neural network approach which allows us to efficiently calculate the conditional version for both neural networks and other regression models, and which properly considers the dependence structure in the feature components. This proposal is also useful to provide drop1 and anova analyses in complex regression models which are similar to their generalized linear model (GLM) counterparts, and we provide a partial dependence plot (PDP) counterpart that considers the right dependence structure in the feature components.

Isotonic Recalibration under a Low Signal-to-Noise Ratio

Insurance pricing systems should fulfill the auto-calibration property to ensure that there is no systematic cross-financing between different price cohorts. Often, regression models are not auto-calibrated. We propose to apply isotonic recalibration to a given regression model to ensure auto-calibration. Our main result proves that under a low signal-to-noise ratio, this isotonic recalibration step leads to explainable pricing systems because the resulting isotonically recalibrated regression functions have a low complexity.

A Discussion of Discrimination and Fairness in Insurance Pricing

Indirect discrimination is an issue of major concern in algorithmic models. This is particularly the case in insurance pricing where protected policyholder characteristics are not allowed to be used for insurance pricing. Simply disregarding protected policyholder information is not an appropriate solution because this still allows for the possibility of inferring the protected characteristics from the non-protected ones. This leads to so-called proxy or indirect discrimination. Though proxy discrimination is qualitatively different from the group fairness concepts in machine learning, these group fairness concepts are proposed to 'smooth out' the impact of protected characteristics in the calculation of insurance prices. The purpose of this note is to share some thoughts about group fairness concepts in the light of insurance pricing and to discuss their implications. We present a statistical model that is free of proxy discrimination, thus, unproblematic from an insurance pricing point of view. However, we find that the canonical price in this statistical model does not satisfy any of the three most popular group fairness axioms. This seems puzzling and we welcome feedback on our example and on the usefulness of these group fairness axioms for non-discriminatory insurance pricing.

Model selection with Gini indices under auto-calibration

The Gini index does not give a strictly consistent scoring rule in general. Therefore, maximizing the Gini index may lead to wrong decisions. The main issue is that the Gini index is a rank-based score that is not calibration-sensitive. We show that the Gini index allows for strictly consistent scoring if we restrict to the class of auto-calibrated regression models.

A multi-task network approach for calculating discrimination-free insurance prices

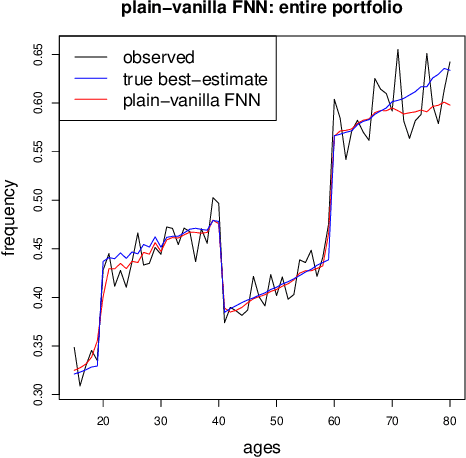
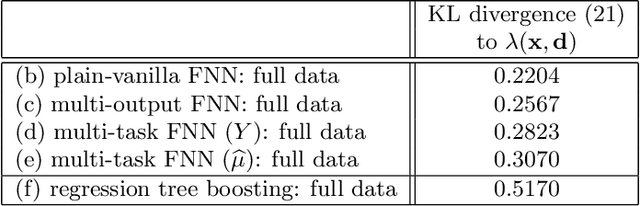
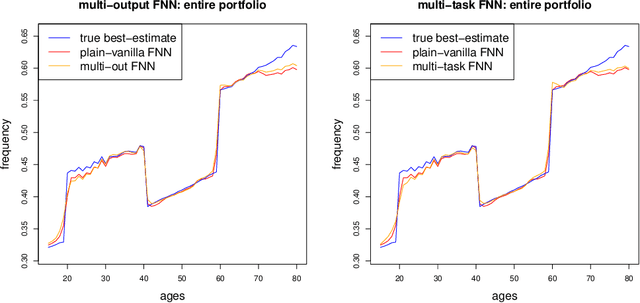
In applications of predictive modeling, such as insurance pricing, indirect or proxy discrimination is an issue of major concern. Namely, there exists the possibility that protected policyholder characteristics are implicitly inferred from non-protected ones by predictive models, and are thus having an undesirable (or illegal) impact on prices. A technical solution to this problem relies on building a best-estimate model using all policyholder characteristics (including protected ones) and then averaging out the protected characteristics for calculating individual prices. However, such approaches require full knowledge of policyholders' protected characteristics, which may in itself be problematic. Here, we address this issue by using a multi-task neural network architecture for claim predictions, which can be trained using only partial information on protected characteristics, and it produces prices that are free from proxy discrimination. We demonstrate the use of the proposed model and we find that its predictive accuracy is comparable to a conventional feedforward neural network (on full information). However, this multi-task network has clearly superior performance in the case of partially missing policyholder information.

LocalGLMnet: interpretable deep learning for tabular data

Deep learning models have gained great popularity in statistical modeling because they lead to very competitive regression models, often outperforming classical statistical models such as generalized linear models. The disadvantage of deep learning models is that their solutions are difficult to interpret and explain, and variable selection is not easily possible because deep learning models solve feature engineering and variable selection internally in a nontransparent way. Inspired by the appealing structure of generalized linear models, we propose a new network architecture that shares similar features as generalized linear models, but provides superior predictive power benefiting from the art of representation learning. This new architecture allows for variable selection of tabular data and for interpretation of the calibrated deep learning model, in fact, our approach provides an additive decomposition in the spirit of Shapley values and integrated gradients.