A functional approach for curve alignment and shape analysis

The shape $\tilde{\mathbf{X}}$ of a random planar curve $\mathbf{X}$ is what remains after removing deformation effects such as scaling, rotation, translation, and parametrization. Previous studies in statistical shape analysis have focused on analyzing $\tilde{\bf X}$ through discrete observations of the curve ${\bf X}$. While this approach has some computational advantages, it overlooks the continuous nature of both ${\bf X}$ and its shape $\tilde{\bf X}$. It also ignores potential dependencies among the deformation variables and their effect on $\tilde{ \bf X}$, which may result in information loss and reduced interpretability. In this paper, we introduce a novel framework for analyzing $\bf X$ in the context of Functional Data Analysis (FDA). Basis expansion techniques are employed to derive analytic solutions for estimating the deformation variables such as rotation and reparametrization, thereby achieving shape alignment. The generative model of $\bf X$ is then investigated using a joint-principal component analysis approach. Numerical experiments on simulated data and the \textit{MPEG-7} database demonstrate that our new approach successfully identifies the deformation parameters and captures the underlying distribution of planar curves in situations where traditional FDA methods fail to do so.

Constructing Ancestral Recombination Graphs through Reinforcement Learning

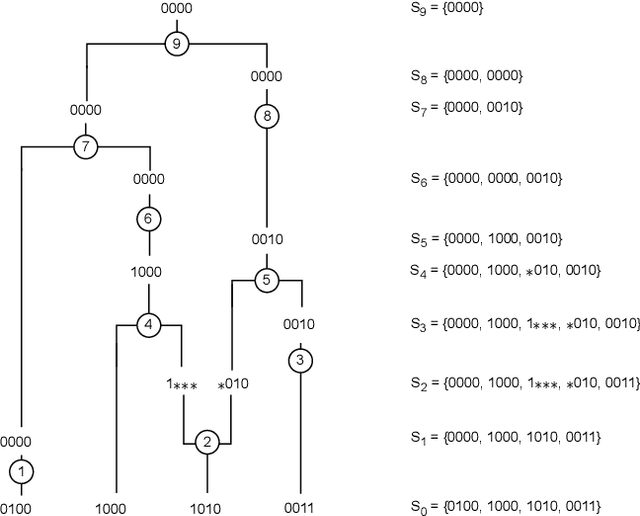
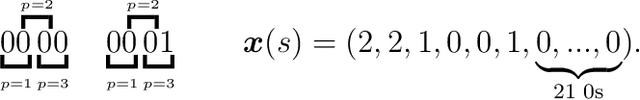
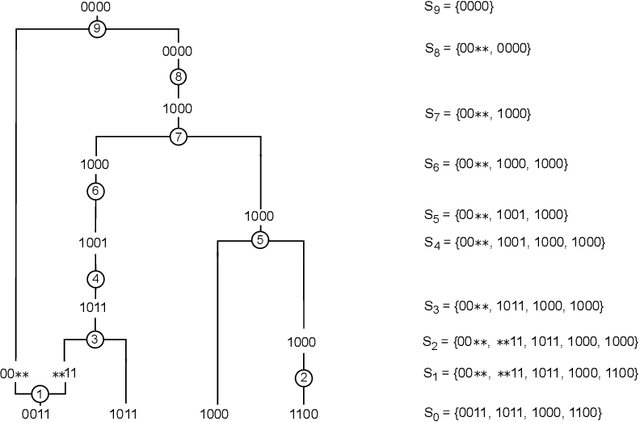
Over the years, many approaches have been proposed to build ancestral recombination graphs (ARGs), graphs used to represent the genetic relationship between individuals. Among these methods, many rely on the assumption that the most likely graph is among the shortest ones. In this paper, we propose a new approach to build short ARGs: Reinforcement Learning (RL). We exploit the similarities between finding the shortest path between a set of genetic sequences and their most recent common ancestor and finding the shortest path between the entrance and exit of a maze, a classic RL problem. In the maze problem, the learner, called the agent, must learn the directions to take in order to escape as quickly as possible, whereas in our problem, the agent must learn the actions to take between coalescence, mutation, and recombination in order to reach the most recent common ancestor as quickly as possible. Our results show that RL can be used to build ARGs as short as those built with a heuristic algorithm optimized to build short ARGs, and sometimes even shorter. Moreover, our method allows to build a distribution of short ARGs for a given sample, and can also generalize learning to new samples not used during the learning process.