Constructing Ancestral Recombination Graphs through Reinforcement Learning
Paper and Code
Jun 17, 2024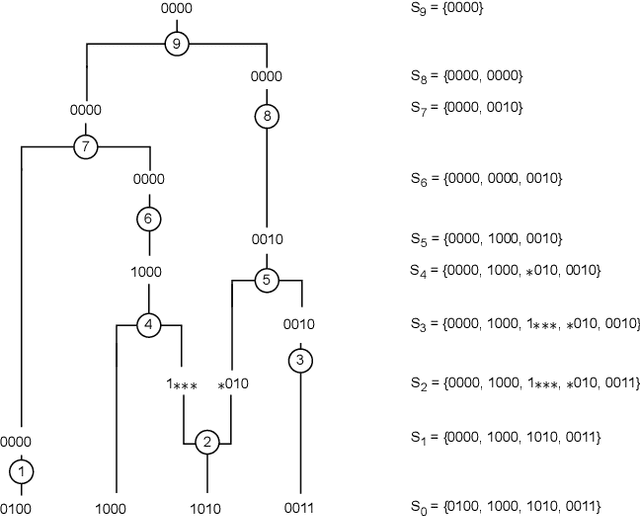

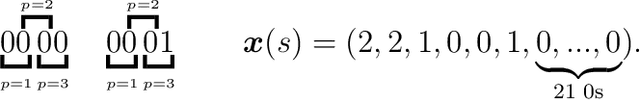
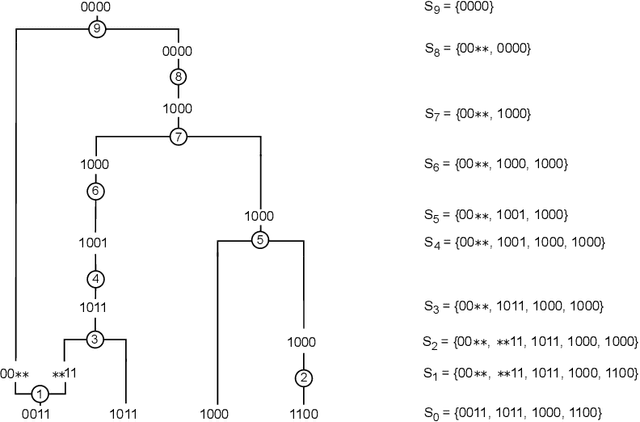
Over the years, many approaches have been proposed to build ancestral recombination graphs (ARGs), graphs used to represent the genetic relationship between individuals. Among these methods, many rely on the assumption that the most likely graph is among the shortest ones. In this paper, we propose a new approach to build short ARGs: Reinforcement Learning (RL). We exploit the similarities between finding the shortest path between a set of genetic sequences and their most recent common ancestor and finding the shortest path between the entrance and exit of a maze, a classic RL problem. In the maze problem, the learner, called the agent, must learn the directions to take in order to escape as quickly as possible, whereas in our problem, the agent must learn the actions to take between coalescence, mutation, and recombination in order to reach the most recent common ancestor as quickly as possible. Our results show that RL can be used to build ARGs as short as those built with a heuristic algorithm optimized to build short ARGs, and sometimes even shorter. Moreover, our method allows to build a distribution of short ARGs for a given sample, and can also generalize learning to new samples not used during the learning process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge