mDAE : modified Denoising AutoEncoder for missing data imputation

This paper introduces a methodology based on Denoising AutoEncoder (DAE) for missing data imputation. The proposed methodology, called mDAE hereafter, results from a modification of the loss function and a straightforward procedure for choosing the hyper-parameters. An ablation study shows on several UCI Machine Learning Repository datasets, the benefit of using this modified loss function and an overcomplete structure, in terms of Root Mean Squared Error (RMSE) of reconstruction. This numerical study is completed by comparing the mDAE methodology with eight other methods (four standard and four more recent). A criterion called Mean Distance to Best (MDB) is proposed to measure how a method performs globally well on all datasets. This criterion is defined as the mean (over the datasets) of the distances between the RMSE of the considered method and the RMSE of the best method. According to this criterion, the mDAE methodology was consistently ranked among the top methods (along with SoftImput and missForest), while the four more recent methods were systematically ranked last. The Python code of the numerical study will be available on GitHub so that results can be reproduced or generalized with other datasets and methods.

From explained variance of correlated components to PCA without orthogonality constraints

Block Principal Component Analysis (Block PCA) of a data matrix A, where loadings Z are determined by maximization of AZ 2 over unit norm orthogonal loadings, is difficult to use for the design of sparse PCA by 1 regularization, due to the difficulty of taking care of both the orthogonality constraint on loadings and the non differentiable 1 penalty. Our objective in this paper is to relax the orthogonality constraint on loadings by introducing new objective functions expvar(Y) which measure the part of the variance of the data matrix A explained by correlated components Y = AZ. So we propose first a comprehensive study of mathematical and numerical properties of expvar(Y) for two existing definitions Zou et al. [2006], Shen and Huang [2008] and four new definitions. Then we show that only two of these explained variance are fit to use as objective function in block PCA formulations for A rid of orthogonality constraints.

ClustGeo: an R package for hierarchical clustering with spatial constraints

In this paper, we propose a Ward-like hierarchical clustering algorithm including spatial/geographical constraints. Two dissimilarity matrices $D_0$ and $D_1$ are inputted, along with a mixing parameter $\alpha \in [0,1]$. The dissimilarities can be non-Euclidean and the weights of the observations can be non-uniform. The first matrix gives the dissimilarities in the "feature space" and the second matrix gives the dissimilarities in the "constraint space". The criterion minimized at each stage is a convex combination of the homogeneity criterion calculated with $D_0$ and the homogeneity criterion calculated with $D_1$. The idea is then to determine a value of $\alpha$ which increases the spatial contiguity without deteriorating too much the quality of the solution based on the variables of interest i.e. those of the feature space. This procedure is illustrated on a real dataset using the R package ClustGeo.

Group-sparse block PCA and explained variance

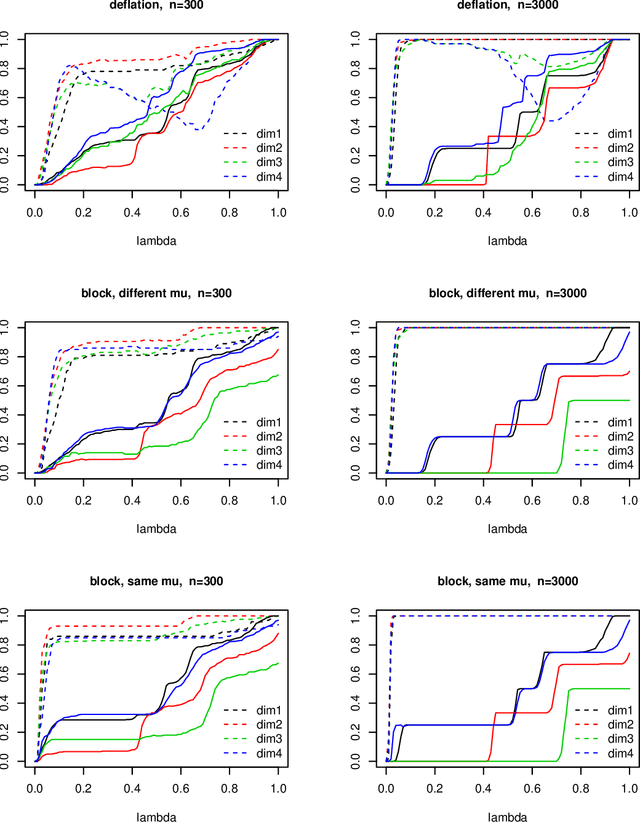
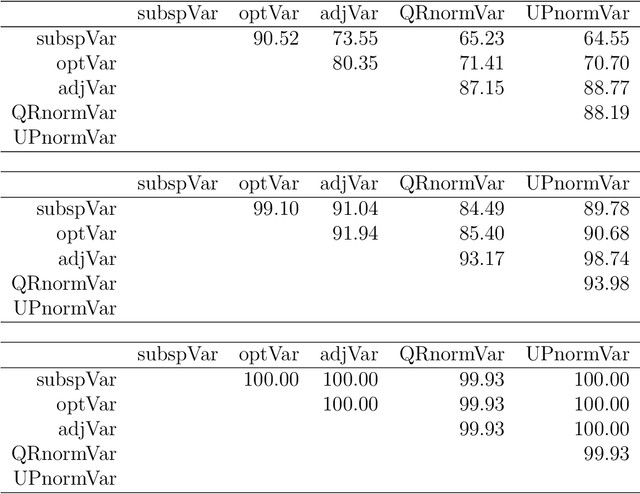
The paper addresses the simultneous determination of goup-sparse loadings by block optimization, and the correlated problem of defining explained variance for a set of non orthogonal components. We give in both cases a comprehensive mathematical presentation of the problem, which leads to propose i) a new formulation/algorithm for group-sparse block PCA and ii) a framework for the definition of explained variance with the analysis of five definitions. The numerical results i) confirm the superiority of block optimization over deflation for the determination of group-sparse loadings, and the importance of group information when available, and ii) show that ranking of algorithms according to explained variance is essentially independant of the definition of explained variance. These results lead to propose a new optimal variance as the definition of choice for explained variance.

On central tendency and dispersion measures for intervals and hypercubes

The uncertainty or the variability of the data may be treated by considering, rather than a single value for each data, the interval of values in which it may fall. This paper studies the derivation of basic description statistics for interval-valued datasets. We propose a geometrical approach in the determination of summary statistics (central tendency and dispersion measures) for interval-valued variables.