From explained variance of correlated components to PCA without orthogonality constraints

Block Principal Component Analysis (Block PCA) of a data matrix A, where loadings Z are determined by maximization of AZ 2 over unit norm orthogonal loadings, is difficult to use for the design of sparse PCA by 1 regularization, due to the difficulty of taking care of both the orthogonality constraint on loadings and the non differentiable 1 penalty. Our objective in this paper is to relax the orthogonality constraint on loadings by introducing new objective functions expvar(Y) which measure the part of the variance of the data matrix A explained by correlated components Y = AZ. So we propose first a comprehensive study of mathematical and numerical properties of expvar(Y) for two existing definitions Zou et al. [2006], Shen and Huang [2008] and four new definitions. Then we show that only two of these explained variance are fit to use as objective function in block PCA formulations for A rid of orthogonality constraints.

Group-sparse block PCA and explained variance

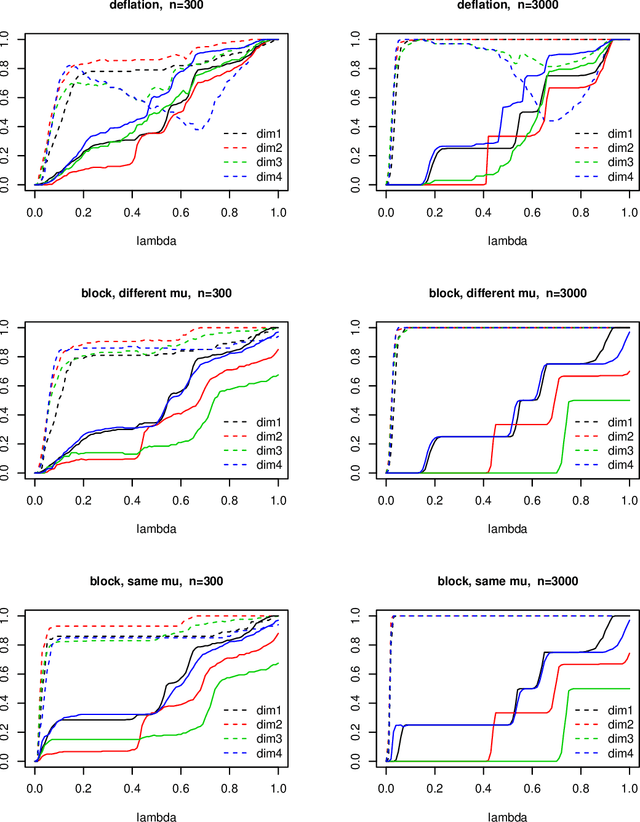
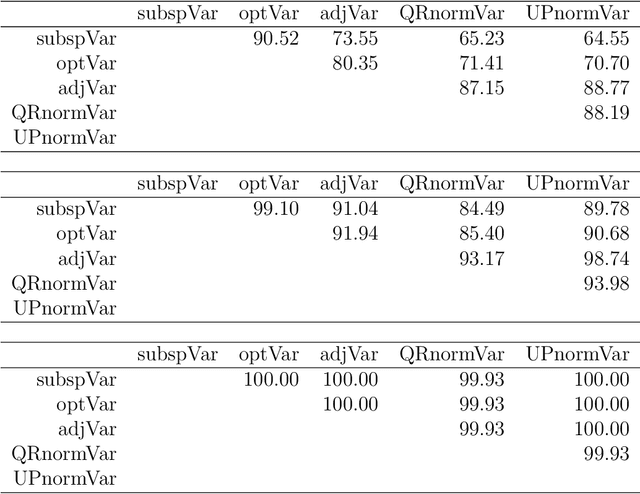
The paper addresses the simultneous determination of goup-sparse loadings by block optimization, and the correlated problem of defining explained variance for a set of non orthogonal components. We give in both cases a comprehensive mathematical presentation of the problem, which leads to propose i) a new formulation/algorithm for group-sparse block PCA and ii) a framework for the definition of explained variance with the analysis of five definitions. The numerical results i) confirm the superiority of block optimization over deflation for the determination of group-sparse loadings, and the importance of group information when available, and ii) show that ranking of algorithms according to explained variance is essentially independant of the definition of explained variance. These results lead to propose a new optimal variance as the definition of choice for explained variance.

Image Segmentation with Multidimensional Refinement Indicators

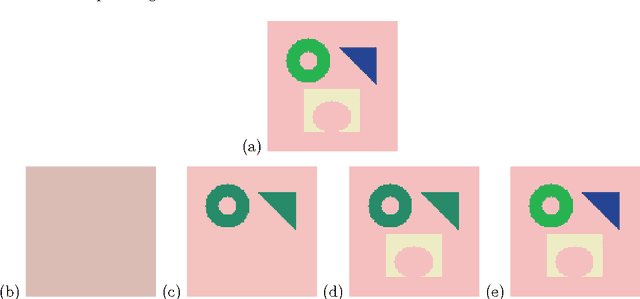
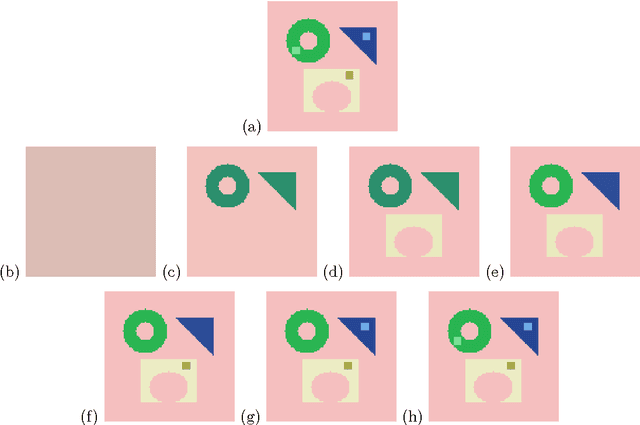
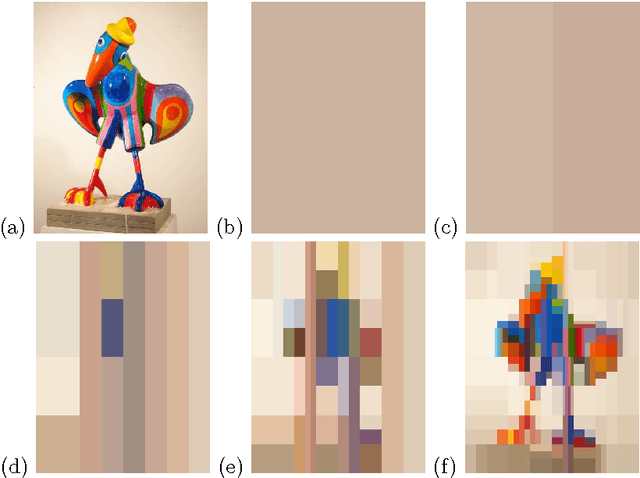
We transpose an optimal control technique to the image segmentation problem. The idea is to consider image segmentation as a parameter estimation problem. The parameter to estimate is the color of the pixels of the image. We use the adaptive parameterization technique which builds iteratively an optimal representation of the parameter into uniform regions that form a partition of the domain, hence corresponding to a segmentation of the image. We minimize an error function during the iterations, and the partition of the image into regions is optimally driven by the gradient of this error. The resulting segmentation algorithm inherits desirable properties from its optimal control origin: soundness, robustness, and flexibility.