DODGE: Ontology-Aware Risk Assessment via Object-Oriented Disruption Graphs

When considering risky events or actions, we must not downplay the role of involved objects: a charged battery in our phone averts the risk of being stranded in the desert after a flat tyre, and a functional firewall mitigates the risk of a hacker intruding the network. The Common Ontology of Value and Risk (COVER) highlights how the role of objects and their relationships remains pivotal to performing transparent, complete and accountable risk assessment. In this paper, we operationalize some of the notions proposed by COVER -- such as parthood between objects and participation of objects in events/actions -- by presenting a new framework for risk assessment: DODGE. DODGE enriches the expressivity of vetted formal models for risk -- i.e., fault trees and attack trees -- by bridging the disciplines of ontology and formal methods into an ontology-aware formal framework composed by a more expressive modelling formalism, Object-Oriented Disruption Graphs (ODGs), logic (ODGLog) and an intermediate query language (ODGLang). With these, DODGE allows risk assessors to pose questions about disruption propagation, disruption likelihood and risk levels, keeping the fundamental role of objects at risk always in sight.

Fuzzy Fault Trees Formalized

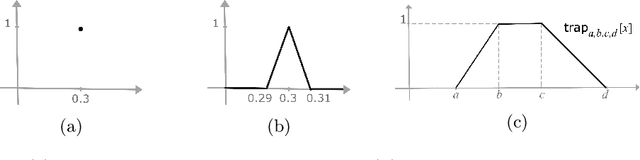
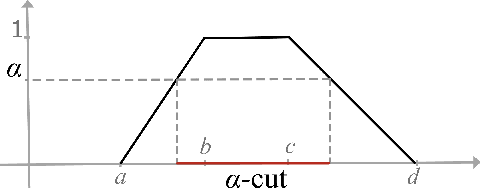
Fault tree analysis is a vital method of assessing safety risks. It helps to identify potential causes of accidents, assess their likelihood and severity, and suggest preventive measures. Quantitative analysis of fault trees is often done via the dependability metrics that compute the system's failure behaviour over time. However, the lack of precise data is a major obstacle to quantitative analysis, and so to reliability analysis. Fuzzy logic is a popular framework for dealing with ambiguous values and has applications in many domains. A number of fuzzy approaches have been proposed to fault tree analysis, but -- to the best of our knowledge -- none of them provide rigorous definitions or algorithms for computing fuzzy unreliability values. In this paper, we define a rigorous framework for fuzzy unreliability values. In addition, we provide a bottom-up algorithm to efficiently calculate fuzzy reliability for a system. The algorithm incorporates the concept of $\alpha$-cuts method. That is, performing binary algebraic operations on intervals on horizontally discretised $\alpha$-cut representations of fuzzy numbers. The method preserves the nonlinearity of fuzzy unreliability. Finally, we illustrate the results obtained from two case studies.