Loss Surface Modality of Feed-Forward Neural Network Architectures

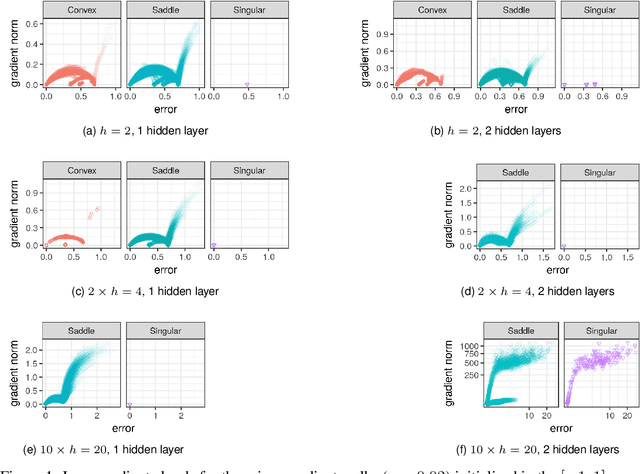
It has been argued in the past that high-dimensional neural networks do not exhibit local minima capable of trapping an optimisation algorithm. However, the relationship between loss surface modality and the neural architecture parameters, such as the number of hidden neurons per layer and the number of hidden layers, remains poorly understood. This study employs fitness landscape analysis to study the modality of neural network loss surfaces under various feed-forward architecture settings. An increase in the problem dimensionality is shown to yield a more searchable and more exploitable loss surface. An increase in the hidden layer width is shown to effectively reduce the number of local minima, and simplify the shape of the global attractor. An increase in the architecture depth is shown to sharpen the global attractor, thus making it more exploitable.

Visualising Basins of Attraction for the Cross-Entropy and the Squared Error Neural Network Loss Functions

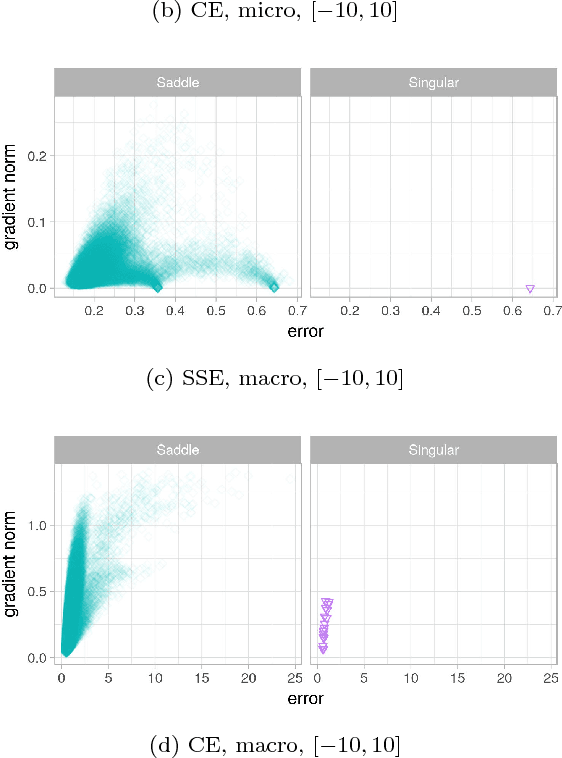
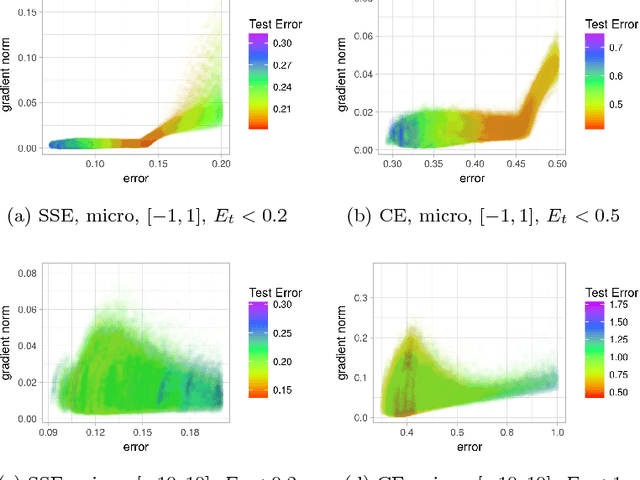
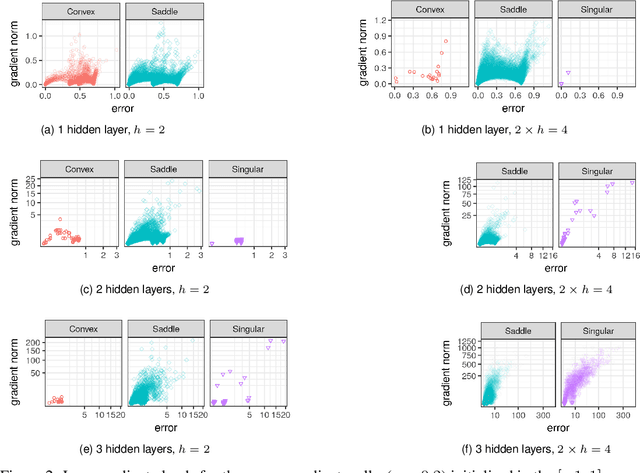
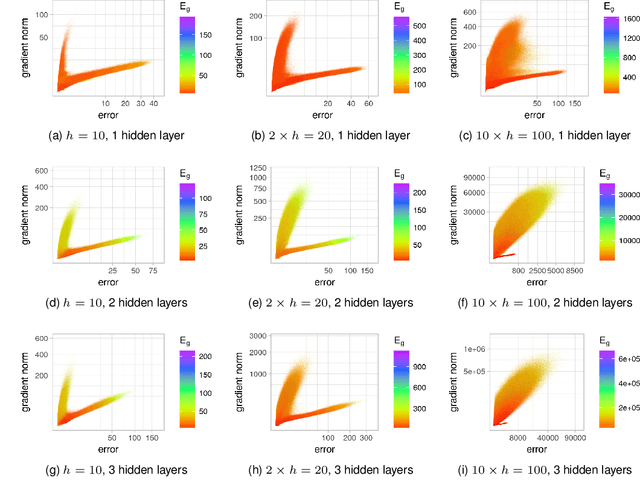
Quantification of the stationary points and the associated basins of attraction of neural network loss surfaces is an important step towards a better understanding of neural network loss surfaces at large. This work proposes a novel method to visualise basins of attraction together with the associated stationary points via gradient-based random sampling. The proposed technique is used to perform an empirical study of the loss surfaces generated by two different error metrics: quadratic loss and entropic loss. The empirical observations confirm the theoretical hypothesis regarding the nature of neural network attraction basins. Entropic loss is shown to exhibit stronger gradients and fewer stationary points than quadratic loss, indicating that entropic loss has a more searchable landscape. Quadratic loss is shown to be more resilient to overfitting than entropic loss. Both losses are shown to exhibit local minima, but the number of local minima is shown to decrease with an increase in dimensionality. Thus, the proposed visualisation technique successfully captures the local minima properties exhibited by the neural network loss surfaces, and can be used for the purpose of fitness landscape analysis of neural networks.