Loss Surface Modality of Feed-Forward Neural Network Architectures
Paper and Code
May 24, 2019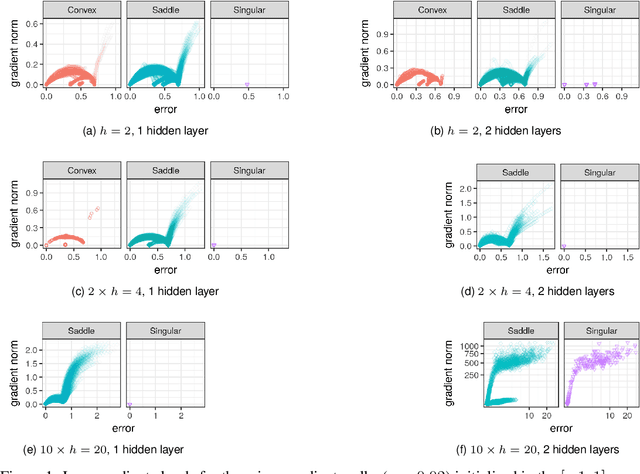
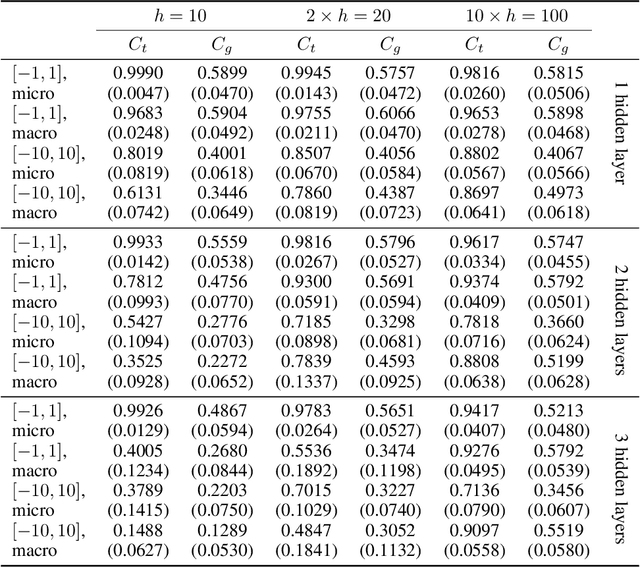
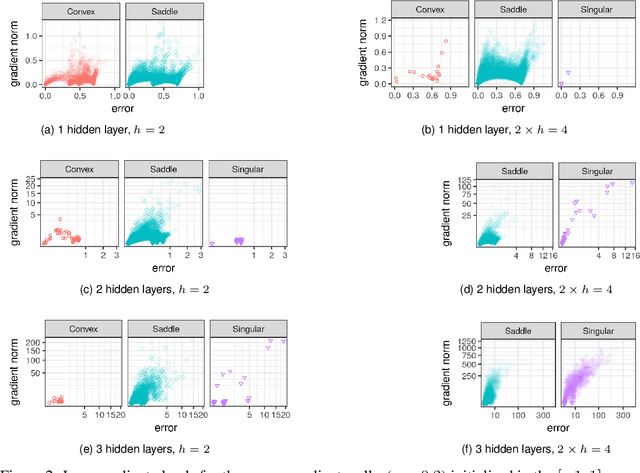
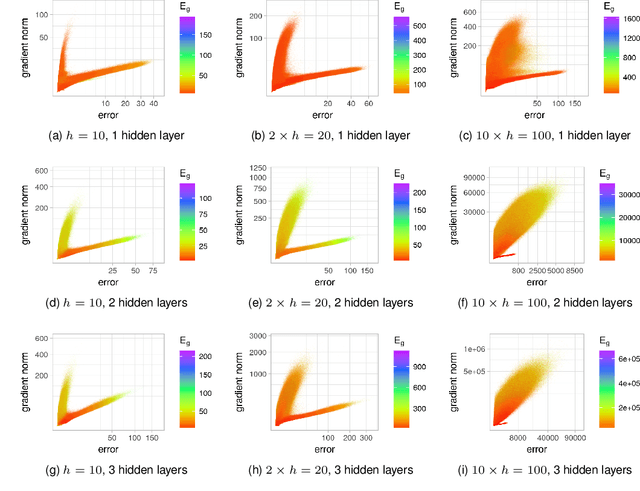
It has been argued in the past that high-dimensional neural networks do not exhibit local minima capable of trapping an optimisation algorithm. However, the relationship between loss surface modality and the neural architecture parameters, such as the number of hidden neurons per layer and the number of hidden layers, remains poorly understood. This study employs fitness landscape analysis to study the modality of neural network loss surfaces under various feed-forward architecture settings. An increase in the problem dimensionality is shown to yield a more searchable and more exploitable loss surface. An increase in the hidden layer width is shown to effectively reduce the number of local minima, and simplify the shape of the global attractor. An increase in the architecture depth is shown to sharpen the global attractor, thus making it more exploitable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge