AXIOM: Learning to Play Games in Minutes with Expanding Object-Centric Models

Current deep reinforcement learning (DRL) approaches achieve state-of-the-art performance in various domains, but struggle with data efficiency compared to human learning, which leverages core priors about objects and their interactions. Active inference offers a principled framework for integrating sensory information with prior knowledge to learn a world model and quantify the uncertainty of its own beliefs and predictions. However, active inference models are usually crafted for a single task with bespoke knowledge, so they lack the domain flexibility typical of DRL approaches. To bridge this gap, we propose a novel architecture that integrates a minimal yet expressive set of core priors about object-centric dynamics and interactions to accelerate learning in low-data regimes. The resulting approach, which we call AXIOM, combines the usual data efficiency and interpretability of Bayesian approaches with the across-task generalization usually associated with DRL. AXIOM represents scenes as compositions of objects, whose dynamics are modeled as piecewise linear trajectories that capture sparse object-object interactions. The structure of the generative model is expanded online by growing and learning mixture models from single events and periodically refined through Bayesian model reduction to induce generalization. AXIOM masters various games within only 10,000 interaction steps, with both a small number of parameters compared to DRL, and without the computational expense of gradient-based optimization.

AutoBayes: A Compositional Framework for Generalized Variational Inference

We introduce a new compositional framework for generalized variational inference, clarifying the different parts of a model, how they interact, and how they compose. We explain that both exact Bayesian inference and the loss functions typical of variational inference (such as variational free energy and its generalizations) satisfy chain rules akin to that of reverse-mode automatic differentiation, and we advocate for exploiting this to build and optimize models accordingly. To this end, we construct a series of compositional tools: for building models; for constructing their inversions; for attaching local loss functions; and for exposing parameters. Finally, we explain how the resulting parameterized statistical games may be optimized locally, too. We illustrate our framework with a number of classic examples, pointing to new areas of extensibility that are revealed.

Star-shaped Tilted Hexarotor Maneuverability: Analysis of the Role of the Tilt Cant Angles

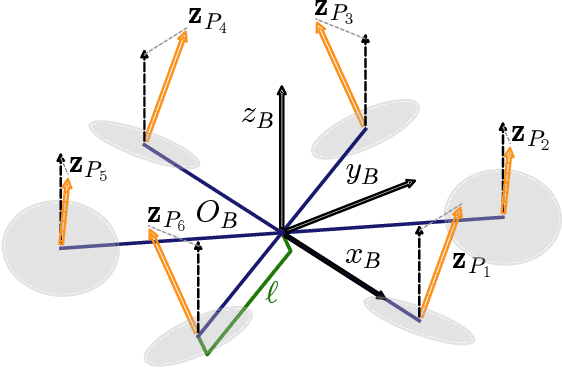
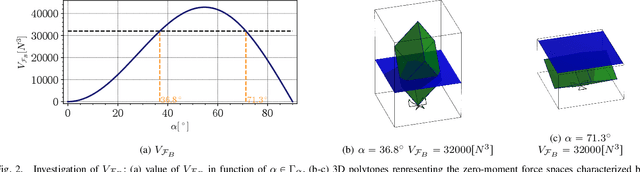
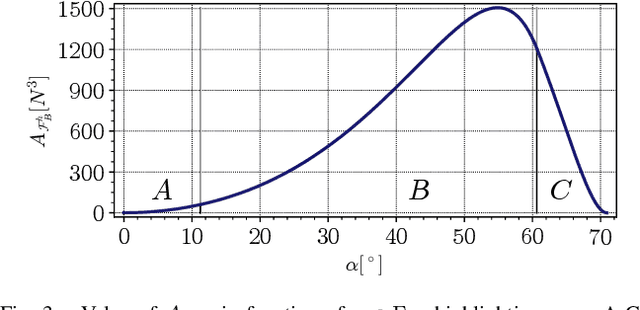
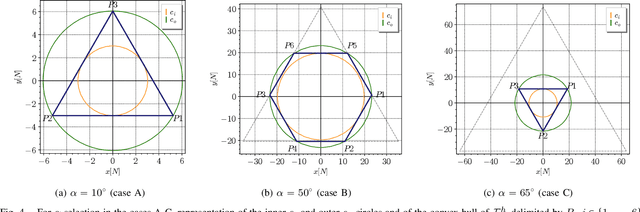
Star-shaped Tilted Hexarotors are rapidly emerging for applications highly demanding in terms of robustness and maneuverability. To ensure improvement in such features, a careful selection of the tilt angles is mandatory. In this work, we present a rigorous analysis of how the force subspace varies with the tilt cant angles, namely the tilt angles along the vehicle arms, taking into account gravity compensation and torque decoupling to abide by the hovering condition. Novel metrics are introduced to assess the performance of existing tilted platforms, as well as to provide some guidelines for the selection of the tilt cant angle in the design phase.