Approximate Joint Diagonalization and Geometric Mean of Symmetric Positive Definite Matrices

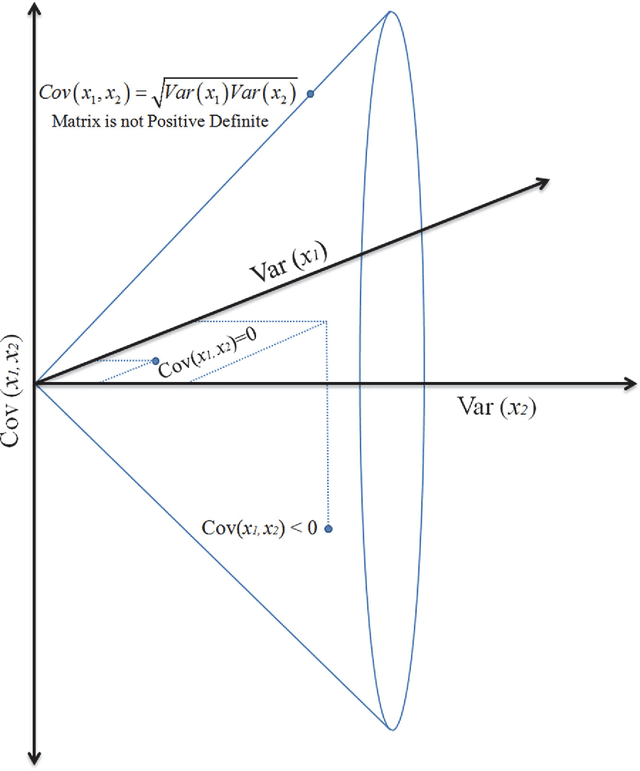
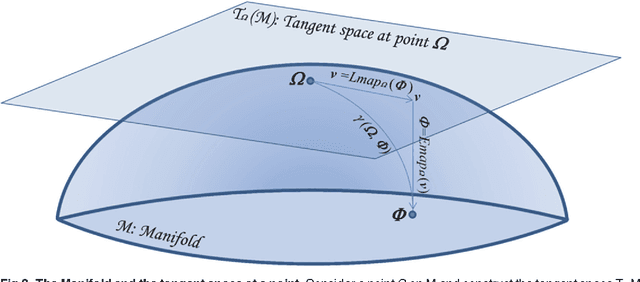
We explore the connection between two problems that have arisen independently in the signal processing and related fields: the estimation of the geometric mean of a set of symmetric positive definite (SPD) matrices and their approximate joint diagonalization (AJD). Today there is a considerable interest in estimating the geometric mean of a SPD matrix set in the manifold of SPD matrices endowed with the Fisher information metric. The resulting mean has several important invariance properties and has proven very useful in diverse engineering applications such as biomedical and image data processing. While for two SPD matrices the mean has an algebraic closed form solution, for a set of more than two SPD matrices it can only be estimated by iterative algorithms. However, none of the existing iterative algorithms feature at the same time fast convergence, low computational complexity per iteration and guarantee of convergence. For this reason, recently other definitions of geometric mean based on symmetric divergence measures, such as the Bhattacharyya divergence, have been considered. The resulting means, although possibly useful in practice, do not satisfy all desirable invariance properties. In this paper we consider geometric means of co-variance matrices estimated on high-dimensional time-series, assuming that the data is generated according to an instantaneous mixing model, which is very common in signal processing. We show that in these circumstances we can approximate the Fisher information geometric mean by employing an efficient AJD algorithm. Our approximation is in general much closer to the Fisher information geometric mean as compared to its competitors and verifies many invariance properties. Furthermore, convergence is guaranteed, the computational complexity is low and the convergence rate is quadratic. The accuracy of this new geometric mean approximation is demonstrated by means of simulations.

A Plug&Play P300 BCI Using Information Geometry

This paper presents a new classification methods for Event Related Potentials (ERP) based on an Information geometry framework. Through a new estimation of covariance matrices, this work extend the use of Riemannian geometry, which was previously limited to SMR-based BCI, to the problem of classification of ERPs. As compared to the state-of-the-art, this new method increases performance, reduces the number of data needed for the calibration and features good generalisation across sessions and subjects. This method is illustrated on data recorded with the P300-based game brain invaders. Finally, an online and adaptive implementation is described, where the BCI is initialized with generic parameters derived from a database and continuously adapt to the individual, allowing the user to play the game without any calibration while keeping a high accuracy.

Mixed-norm Regularization for Brain Decoding

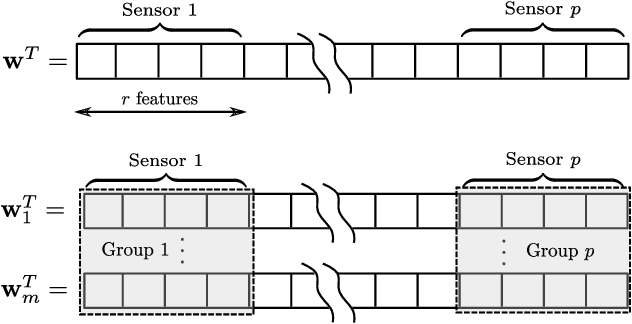
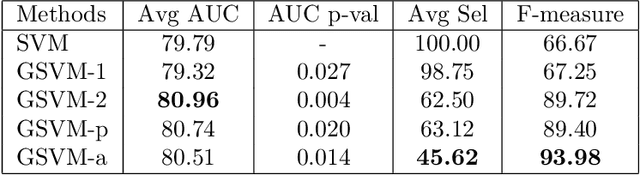
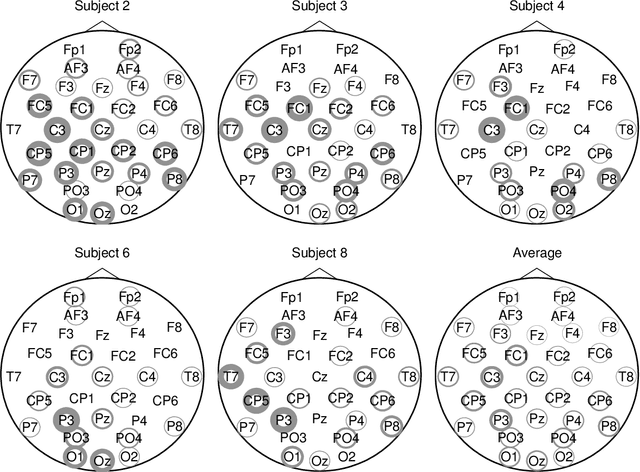
This work investigates the use of mixed-norm regularization for sensor selection in Event-Related Potential (ERP) based Brain-Computer Interfaces (BCI). The classification problem is cast as a discriminative optimization framework where sensor selection is induced through the use of mixed-norms. This framework is extended to the multi-task learning situation where several similar classification tasks related to different subjects are learned simultaneously. In this case, multi-task learning helps in leveraging data scarcity issue yielding to more robust classifiers. For this purpose, we have introduced a regularizer that induces both sensor selection and classifier similarities. The different regularization approaches are compared on three ERP datasets showing the interest of mixed-norm regularization in terms of sensor selection. The multi-task approaches are evaluated when a small number of learning examples are available yielding to significant performance improvements especially for subjects performing poorly.