Probabilistic Performance-Pattern Decomposition (PPPD): analysis framework and applications to stochastic mechanical systems

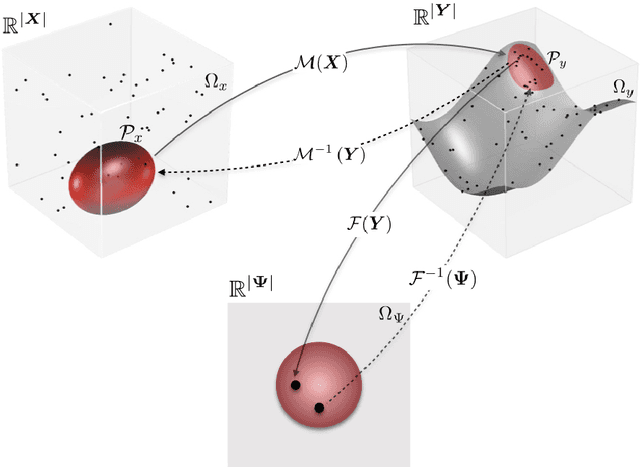
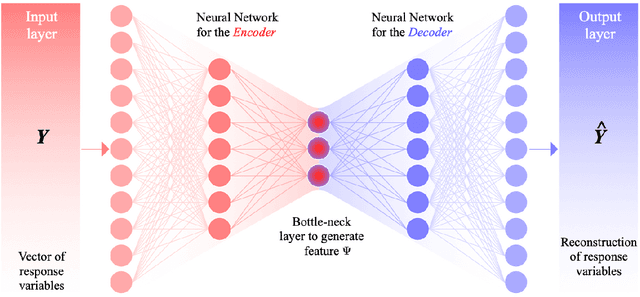
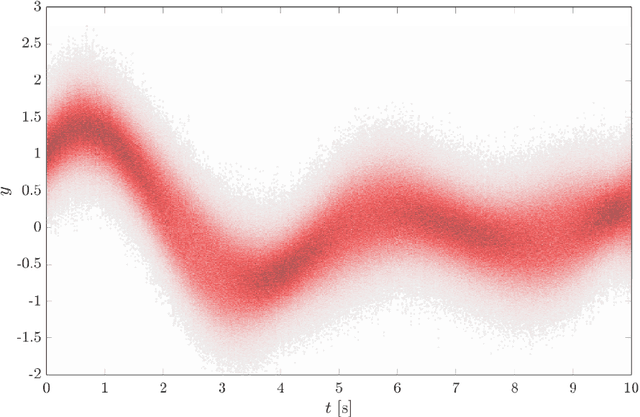
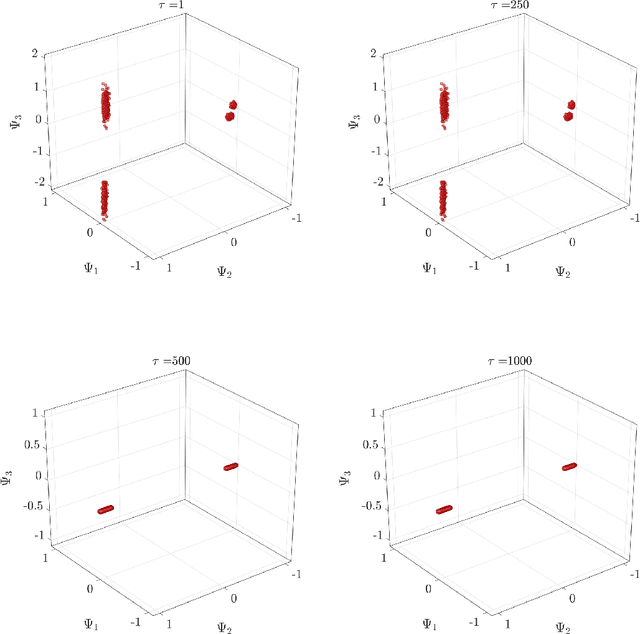
Since the early 1900s, numerous research efforts have been devoted to developing quantitative solutions to stochastic mechanical systems. In general, the problem is perceived as solved when a complete or partial probabilistic description on the quantity of interest (QoI) is determined. However, in the presence of complex system behavior, there is a critical need to go beyond mere probabilistic descriptions. In fact, to gain a full understanding of the system, it is crucial to extract physical characterizations from the probabilistic structure of the QoI, especially when the QoI solution is obtained in a data-driven fashion. Motivated by this perspective, the paper proposes a framework to obtain structuralized characterizations on behaviors of stochastic systems. The framework is named Probabilistic Performance-Pattern Decomposition (PPPD). PPPD analysis aims to decompose complex response behaviors, conditional to a prescribed performance state, into meaningful patterns in the space of system responses, and to investigate how the patterns are triggered in the space of basic random variables. To illustrate the application of PPPD, the paper studies three numerical examples: 1) an illustrative example with hypothetical stochastic processes input and output; 2) a stochastic Lorenz system with periodic as well as chaotic behaviors; and 3) a simplified shear-building model subjected to a stochastic ground motion excitation.

Neural Network Applications in Earthquake Prediction (1994-2019): Meta-Analytic Insight on their Limitations

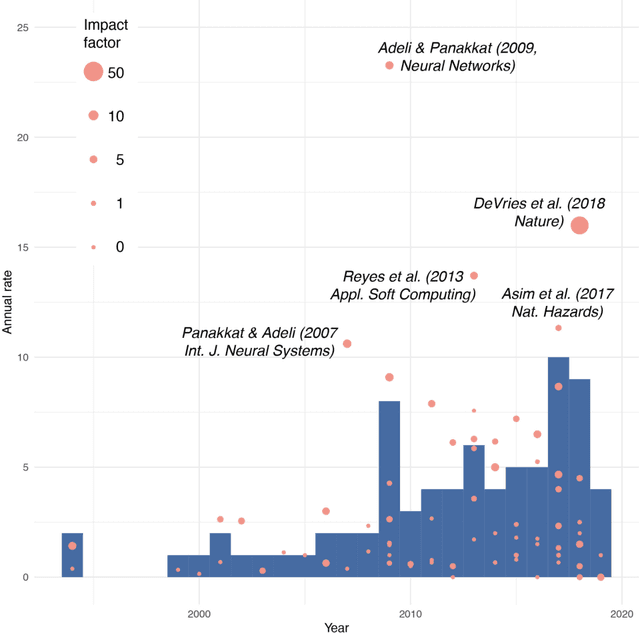
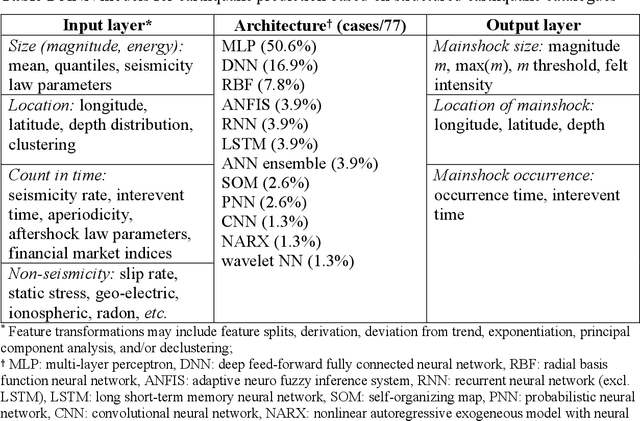
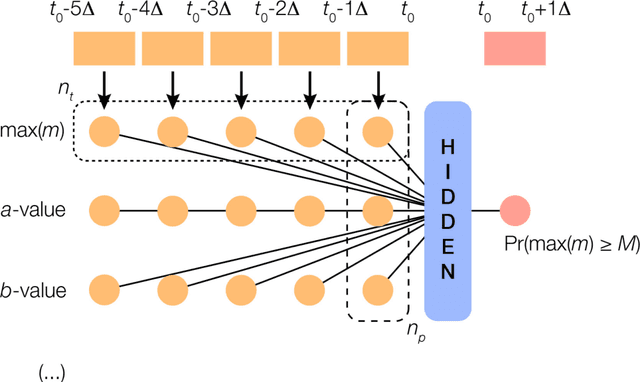
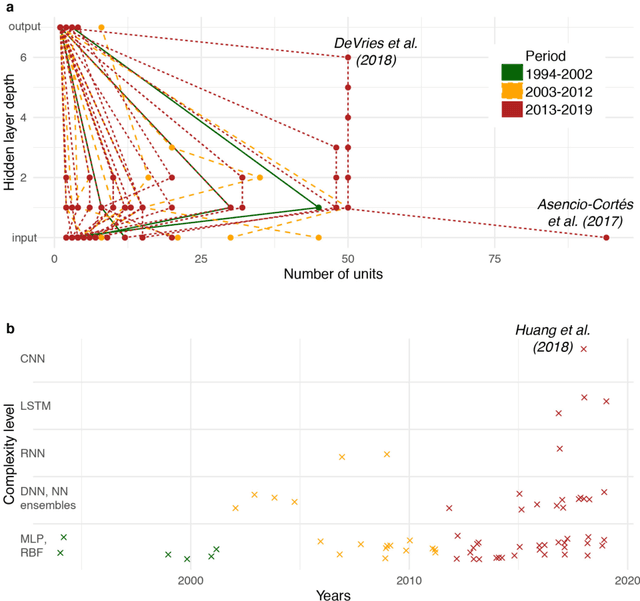
In the last few years, deep learning has solved seemingly intractable problems, boosting the hope to find approximate solutions to problems that now are considered unsolvable. Earthquake prediction, the Grail of Seismology, is, in this context of continuous exciting discoveries, an obvious choice for deep learning exploration. We review the entire literature of artificial neural network (ANN) applications for earthquake prediction (77 articles, 1994-2019 period) and find two emerging trends: an increasing interest in this domain, and a complexification of ANN models over time, towards deep learning. Despite apparent positive results observed in this corpus, we demonstrate that simpler models seem to offer similar predictive powers, if not better ones. Due to the structured, tabulated nature of earthquake catalogues, and the limited number of features so far considered, simpler and more transparent machine learning models seem preferable at the present stage of research. Those baseline models follow first physical principles and are consistent with the known empirical laws of Statistical Seismology, which have minimal abilities to predict large earthquakes.

A novel active learning-based Gaussian process metamodelling strategy for estimating the full probability distribution in forward UQ analysis

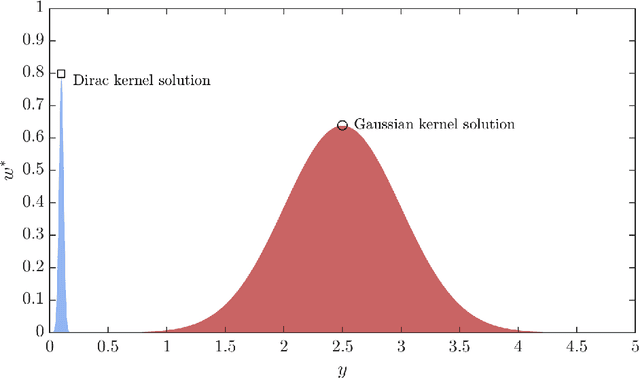
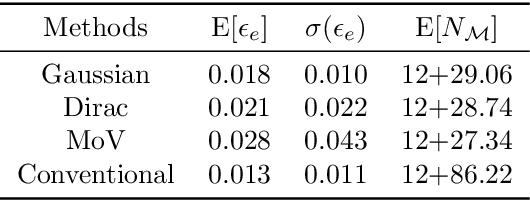
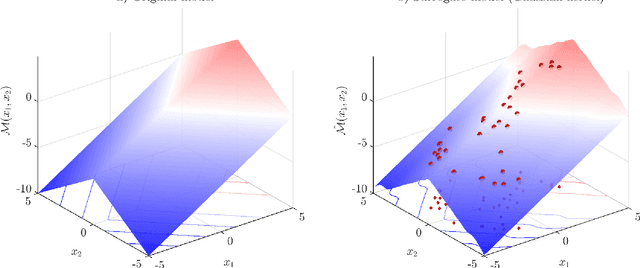
This paper proposes an active learning-based Gaussian process (AL-GP) metamodelling method to estimate the cumulative as well as complementary cumulative distribution function (CDF/CCDF) for forward uncertainty quantification (UQ) problems. Within the field of UQ, previous studies focused on developing AL-GP approaches for reliability (rare event probability) analysis of expensive black-box solvers. A naive iteration of these algorithms with respect to different CDF/CCDF threshold values would yield a discretized CDF/CCDF. However, this approach inevitably leads to a trade-off between accuracy and computational efficiency since both depend (in opposite way) on the selected discretization. In this study, a specialized error measure and a learning function are developed such that the resulting AL-GP method is able to efficiently estimate the CDF/CCDF for a specified range of interest without an explicit dependency on discretization. Particularly, the proposed AL-GP method is able to simultaneously provide accurate CDF and CCDF estimation in their median-low probability regions. Three numerical examples are introduced to test and verify the proposed method.