Networks with Finite VC Dimension: Pro and Contra

Approximation and learning of classifiers of large data sets by neural networks in terms of high-dimensional geometry and statistical learning theory are investigated. The influence of the VC dimension of sets of input-output functions of networks on approximation capabilities is compared with its influence on consistency in learning from samples of data. It is shown that, whereas finite VC dimension is desirable for uniform convergence of empirical errors, it may not be desirable for approximation of functions drawn from a probability distribution modeling the likelihood that they occur in a given type of application. Based on the concentration-of-measure properties of high dimensional geometry, it is proven that both errors in approximation and empirical errors behave almost deterministically for networks implementing sets of input-output functions with finite VC dimensions in processing large data sets. Practical limitations of the universal approximation property, the trade-offs between the accuracy of approximation and consistency in learning from data, and the influence of depth of networks with ReLU units on their accuracy and consistency are discussed.

An efficient combined local and global search strategy for optimization of parallel kinematic mechanisms with joint limits and collision constraints

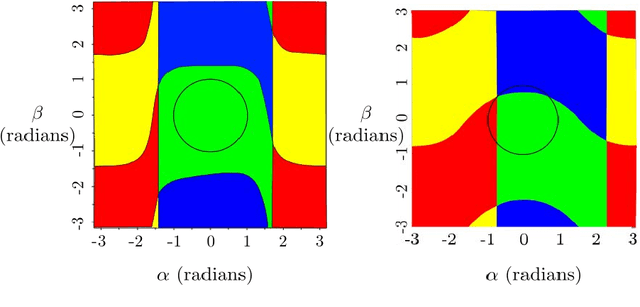
The optimization of parallel kinematic manipulators (PKM) involve several constraints that are difficult to formalize, thus making optimal synthesis problem highly challenging. The presence of passive joint limits as well as the singularities and self-collisions lead to a complicated relation between the input and output parameters. In this article, a novel optimization methodology is proposed by combining a local search, Nelder-Mead algorithm, with global search methodologies such as low discrepancy distribution for faster and more efficient exploration of the optimization space. The effect of the dimension of the optimization problem and the different constraints are discussed to highlight the complexities of closed-loop kinematic chain optimization. The work also presents the approaches used to consider constraints for passive joint boundaries as well as singularities to avoid internal collisions in such mechanisms. The proposed algorithm can also optimize the length of the prismatic actuators and the constraints can be added in modular fashion, allowing to understand the impact of given criteria on the final result. The application of the presented approach is used to optimize two PKMs of different degrees of freedom.