LogitBoost autoregressive networks

Multivariate binary distributions can be decomposed into products of univariate conditional distributions. Recently popular approaches have modeled these conditionals through neural networks with sophisticated weight-sharing structures. It is shown that state-of-the-art performance on several standard benchmark datasets can actually be achieved by training separate probability estimators for each dimension. In that case, model training can be trivially parallelized over data dimensions. On the other hand, complexity control has to be performed for each learned conditional distribution. Three possible methods are considered and experimentally compared. The estimator that is employed for each conditional is LogitBoost. Similarities and differences between the proposed approach and autoregressive models based on neural networks are discussed in detail.

Dynamic Partition Models

We present a new approach for learning compact and intuitive distributed representations with binary encoding. Rather than summing up expert votes as in products of experts, we employ for each variable the opinion of the most reliable expert. Data points are hence explained through a partitioning of the variables into expert supports. The partitions are dynamically adapted based on which experts are active. During the learning phase we adopt a smoothed version of this model that uses separate mixtures for each data dimension. In our experiments we achieve accurate reconstructions of high-dimensional data points with at most a dozen experts.

Compact Compositional Models

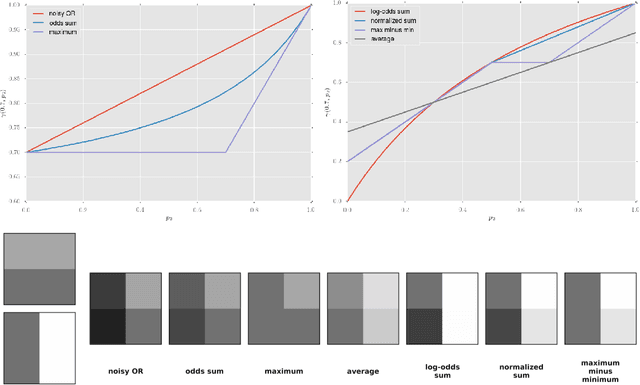
Learning compact and interpretable representations is a very natural task, which has not been solved satisfactorily even for simple binary datasets. In this paper, we review various ways of composing experts for binary data and argue that competitive forms of interaction are best suited to learn low-dimensional representations. We propose a new composition rule that discourages experts from focusing on similar structures and that penalizes opposing votes strongly so that abstaining from voting becomes more attractive. We also introduce a novel sequential initialization procedure, which is based on a process of oversimplification and correction. Experiments show that with our approach very intuitive models can be learned.

Mixtures of Sparse Autoregressive Networks

We consider high-dimensional distribution estimation through autoregressive networks. By combining the concepts of sparsity, mixtures and parameter sharing we obtain a simple model which is fast to train and which achieves state-of-the-art or better results on several standard benchmark datasets. Specifically, we use an L1-penalty to regularize the conditional distributions and introduce a procedure for automatic parameter sharing between mixture components. Moreover, we propose a simple distributed representation which permits exact likelihood evaluations since the latent variables are interleaved with the observable variables and can be easily integrated out. Our model achieves excellent generalization performance and scales well to extremely high dimensions.

Directional Decision Lists

In this paper we introduce a novel family of decision lists consisting of highly interpretable models which can be learned efficiently in a greedy manner. The defining property is that all rules are oriented in the same direction. Particular examples of this family are decision lists with monotonically decreasing (or increasing) probabilities. On simulated data we empirically confirm that the proposed model family is easier to train than general decision lists. We exemplify the practical usability of our approach by identifying problem symptoms in a manufacturing process.