Manuel A. Roehrl
Modeling System Dynamics with Physics-Informed Neural Networks Based on Lagrangian Mechanics
May 29, 2020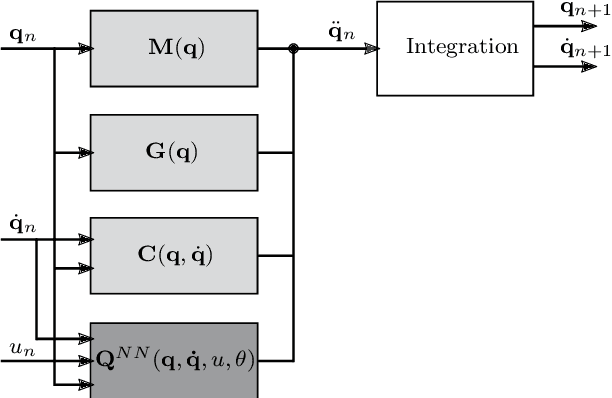
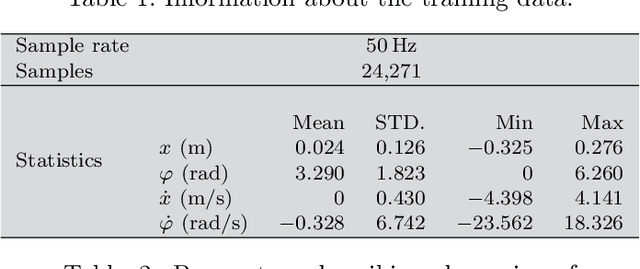

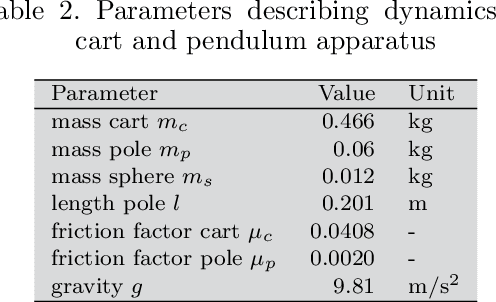
Abstract:Identifying accurate dynamic models is required for the simulation and control of various technical systems. In many important real-world applications, however, the two main modeling approaches often fail to meet requirements: first principles methods suffer from high bias, whereas data-driven modeling tends to have high variance. Additionally, purely data-based models often require large amounts of data and are often difficult to interpret. In this paper, we present physics-informed neural ordinary differential equations (PINODE), a hybrid model that combines the two modeling techniques to overcome the aforementioned problems. This new approach directly incorporates the equations of motion originating from the Lagrange Mechanics into a deep neural network structure. Thus, we can integrate prior physics knowledge where it is available and use function approximation--e. g., neural networks--where it is not. The method is tested with a forward model of a real-world physical system with large uncertainties. The resulting model is accurate and data-efficient while ensuring physical plausibility. With this, we demonstrate a method that beneficially merges physical insight with real data. Our findings are of interest for model-based control and system identification of mechanical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge