Non-convex regularization based on shrinkage penalty function

Total Variation regularization (TV) is a seminal approach for image recovery. TV involves the norm of the image's gradient, aggregated over all pixel locations. Therefore, TV leads to piece-wise constant solutions, resulting in what is known as the "staircase effect." To mitigate this effect, the Hessian Schatten norm regularization (HSN) employs second-order derivatives, represented by the pth norm of eigenvalues in the image hessian, summed across all pixels. HSN demonstrates superior structure-preserving properties compared to TV. However, HSN solutions tend to be overly smoothed. To address this, we introduce a non-convex shrinkage penalty applied to the Hessian's eigenvalues, deviating from the convex lp norm. It is important to note that the shrinkage penalty is not defined directly in closed form, but specified indirectly through its proximal operation. This makes constructing a provably convergent algorithm difficult as the singular values are also defined through a non-linear operation. However, we were able to derive a provably convergent algorithm using proximal operations. We prove the convergence by establishing that the proposed regularization adheres to restricted proximal regularity. The images recovered by this regularization were sharper than the convex counterparts.

Compact Representation of n-th order TGV

Although regularization methods based on derivatives are favored for their robustness and computational simplicity, research exploring higher-order derivatives remains limited. This scarcity can possibly be attributed to the appearance of oscillations in reconstructions when directly generalizing TV-1 to higher orders (3 or more). Addressing this, Bredies et. al introduced a notable approach for generalizing total variation, known as Total Generalized Variation (TGV). This technique introduces a regularization that generates estimates embodying piece-wise polynomial behavior of varying degrees across distinct regions of an image.Importantly, to our current understanding, no sufficiently general algorithm exists for solving TGV regularization for orders beyond 2. This is likely because of two problems: firstly, the problem is complex as TGV regularization is defined as a minimization problem with non-trivial constraints, and secondly, TGV is represented in terms of tensor-fields which is difficult to implement. In this work we tackle the first challenge by giving two simple and implementable representations of n th order TGV

Generalized Hessian-Schatten Norm Regularization for Image Reconstruction

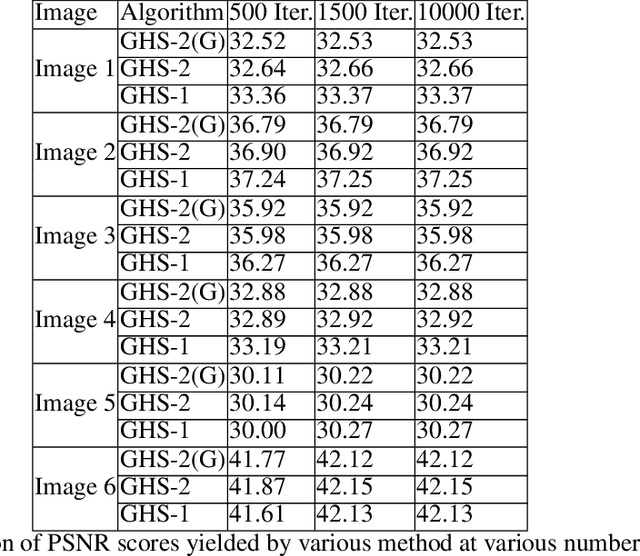
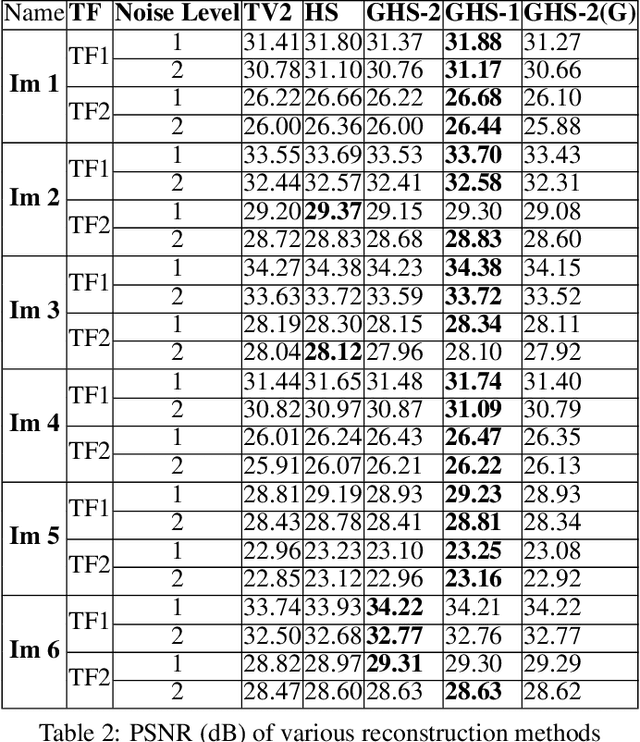
Regularization plays a crucial role in reliably utilizing imaging systems for scientific and medical investigations. It helps to stabilize the process of computationally undoing any degradation caused by physical limitations of the imaging process. In the past decades, total variation regularization, especially second-order total variation (TV-2) regularization played a dominant role in the literature. Two forms of generalizations, namely Hessian-Schatten norm (HSN) regularization, and total generalized variation (TGV) regularization, have been recently proposed and have become significant developments in the area of regularization for imaging inverse problems owing to their performance. Here, we develop a novel regularization for image recovery that combines the strengths of these well-known forms. We achieve this by restricting the maximization space in the dual form of HSN in the same way that TGV is obtained from TV-2. We name the new regularization as the generalized Hessian-Schatten norm regularization (GHSN), and we develop a novel optimization method for image reconstruction using the new form of regularization based on the well-known framework called alternating direction method of multipliers (ADMM). We demonstrate the strength of the GHSN using some reconstruction examples.