PSTAIC regularization for 2D spatiotemporal image reconstruction

We propose a model for restoration of spatio-temporal TIRF images based on infimal decomposition regularization model named STAIC proposed earlier. We propose to strengthen the STAIC algorithm by enabling it to estimate the relative weights in the regularization term by incorporating it as part of the optimization problem. We also design an iterative scheme which alternatively minimizes the weight and image sub-problems. We demonstrate the restoration quality of this regularization scheme against other restoration models enabled by similar weight estimation schemes.

STAIC regularization for spatio-temporal image reconstruction

We propose a regularization-based image restoration scheme for 2D images recorded over time (2D+t). We design an infimal convolution-based regularization function which we call spatio-temporal Adaptive Infimal Convolution (STAIC) regularization. We formulate the infimal convolution in the form of an additive decomposition of the 2D+t image such that the extent of spatial and temporal smoothing is controlled in a spatially and temporally varying manner. This makes the regularization adaptable to the local characteristics of the motion leading to an improved ability to handle noise. We also develop a minimization method for image reconstruction by using the proposed form of regularization. We demonstrate the effectiveness of the proposed regularization using TIRF images recorded over time and compare with some selected existing regularizations.

Generalized Hessian-Schatten Norm Regularization for Image Reconstruction

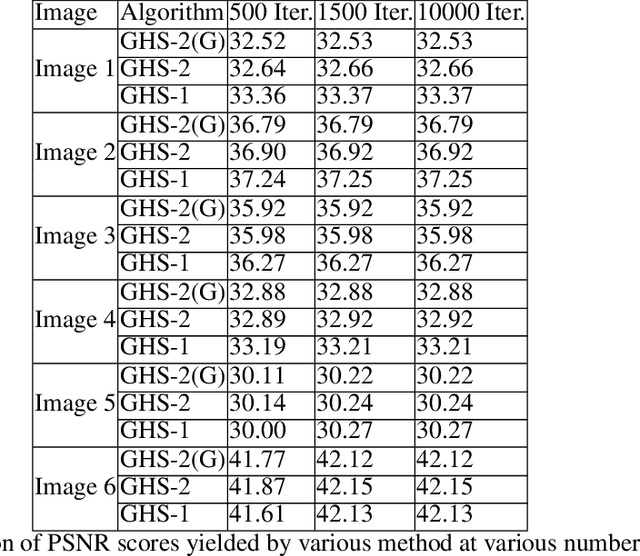
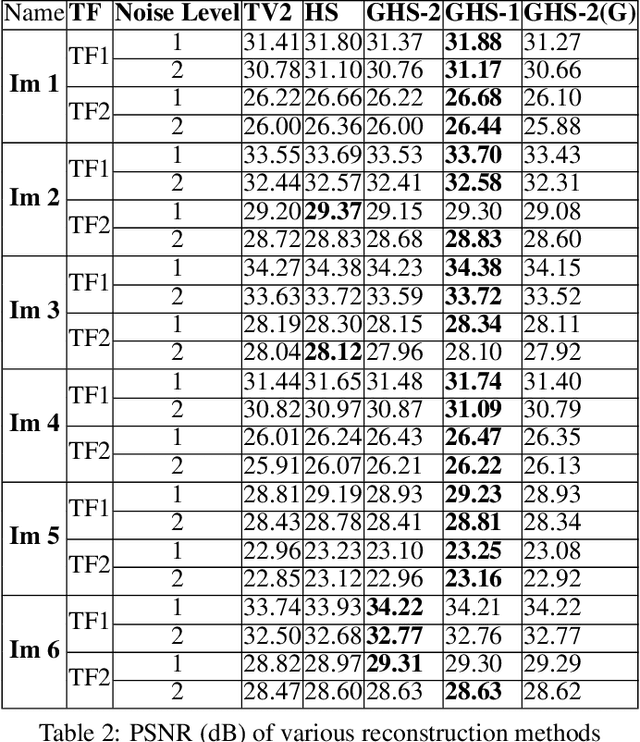
Regularization plays a crucial role in reliably utilizing imaging systems for scientific and medical investigations. It helps to stabilize the process of computationally undoing any degradation caused by physical limitations of the imaging process. In the past decades, total variation regularization, especially second-order total variation (TV-2) regularization played a dominant role in the literature. Two forms of generalizations, namely Hessian-Schatten norm (HSN) regularization, and total generalized variation (TGV) regularization, have been recently proposed and have become significant developments in the area of regularization for imaging inverse problems owing to their performance. Here, we develop a novel regularization for image recovery that combines the strengths of these well-known forms. We achieve this by restricting the maximization space in the dual form of HSN in the same way that TGV is obtained from TV-2. We name the new regularization as the generalized Hessian-Schatten norm regularization (GHSN), and we develop a novel optimization method for image reconstruction using the new form of regularization based on the well-known framework called alternating direction method of multipliers (ADMM). We demonstrate the strength of the GHSN using some reconstruction examples.