Man-Yau Chiu
Efficient Likelihood Bayesian Constrained Local Model
Nov 30, 2016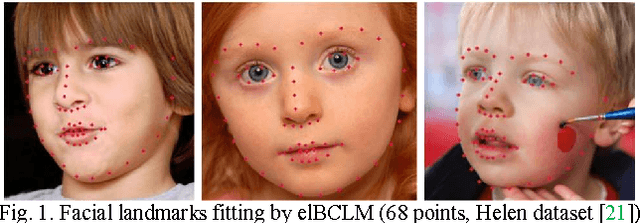
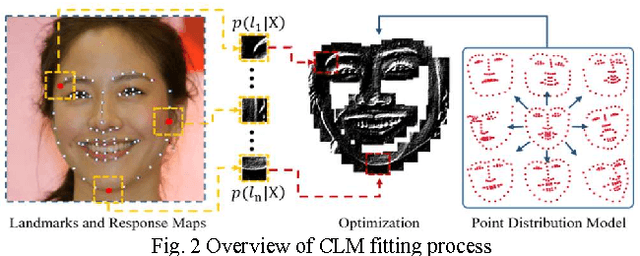
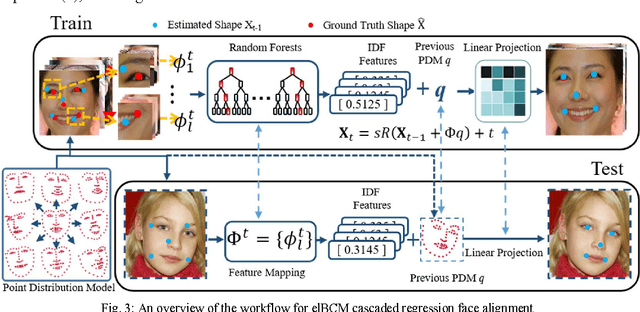
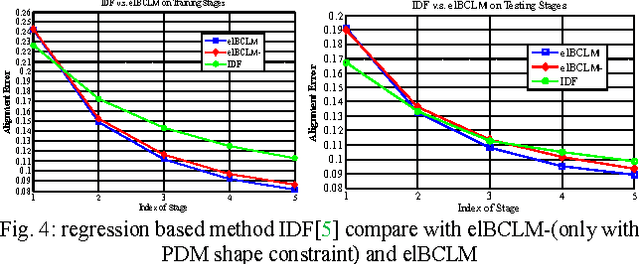
Abstract:The constrained local model (CLM) proposes a paradigm that the locations of a set of local landmark detectors are constrained to lie in a subspace, spanned by a shape point distribution model (PDM). Fitting the model to an object involves two steps. A response map, which represents the likelihood of the location of a landmark, is first computed for each landmark using local-texture detectors. Then, an optimal PDM is determined by jointly maximizing all the response maps simultaneously, with a global shape constraint. This global optimization can be considered as a Bayesian inference problem, where the posterior distribution of the shape parameters, as well as the pose parameters, can be inferred using maximum a posteriori (MAP). In this paper, we present a cascaded face-alignment approach, which employs random-forest regressors to estimate the positions of each landmark, as a likelihood term, efficiently in the CLM model. Interpretation from CLM framework, this algorithm is named as an efficient likelihood Bayesian constrained local model (elBCLM). Furthermore, in each stage of the regressors, the PDM non-rigid parameters of previous stage can work as shape clues for training each stage regressors. Experimental results on benchmarks show our approach achieve about 3 to 5 times speed-up compared with CLM models and improve around 10% on fitting quality compare with the same setting regression models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge