Solving Travelling Thief Problems using Coordination Based Methods

A travelling thief problem (TTP) is a proxy to real-life problems such as postal collection. TTP comprises an entanglement of a travelling salesman problem (TSP) and a knapsack problem (KP) since items of KP are scattered over cities of TSP, and a thief has to visit cities to collect items. In TTP, city selection and item selection decisions need close coordination since the thief's travelling speed depends on the knapsack's weight and the order of visiting cities affects the order of item collection. Existing TTP solvers deal with city selection and item selection separately, keeping decisions for one type unchanged while dealing with the other type. This separation essentially means very poor coordination between two types of decision. In this paper, we first show that a simple local search based coordination approach does not work in TTP. Then, to address the aforementioned problems, we propose a human designed coordination heuristic that makes changes to collection plans during exploration of cyclic tours. We further propose another human designed coordination heuristic that explicitly exploits the cyclic tours in item selections during collection plan exploration. Lastly, we propose a machine learning based coordination heuristic that captures characteristics of the two human designed coordination heuristics. Our proposed coordination based approaches help our TTP solver significantly outperform existing state-of-the-art TTP solvers on a set of benchmark problems. Our solver is named Cooperation Coordination (CoCo) and its source code is available from https://github.com/majid75/CoCo

Surrogate Assisted Optimisation for Travelling Thief Problems

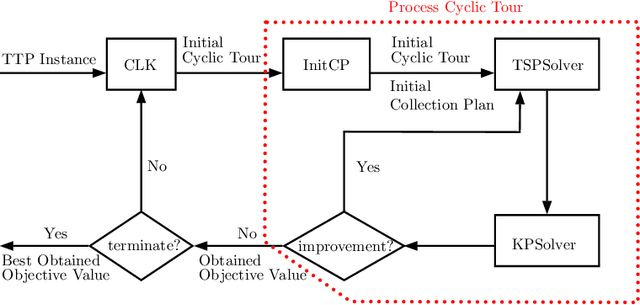
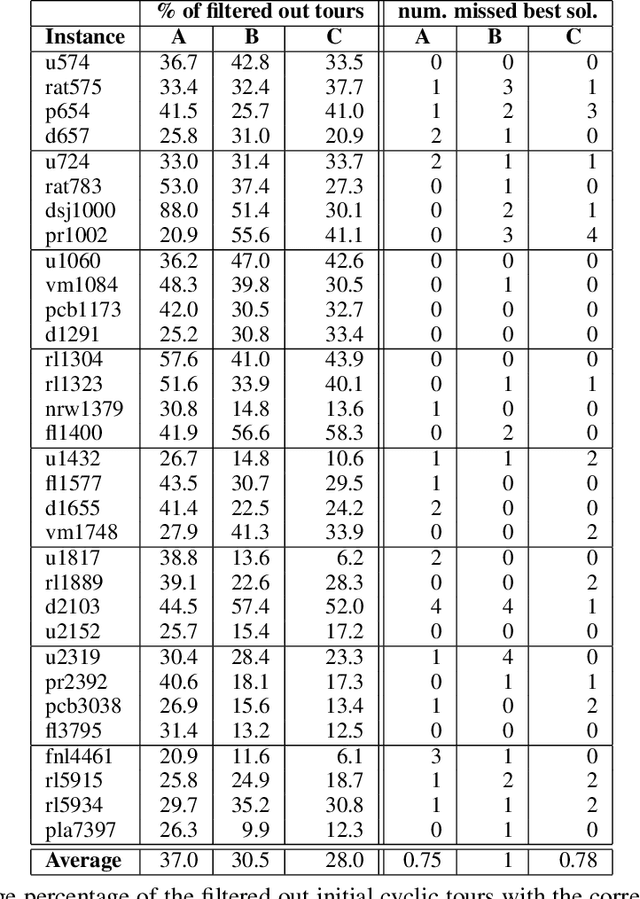
The travelling thief problem (TTP) is a multi-component optimisation problem involving two interdependent NP-hard components: the travelling salesman problem (TSP) and the knapsack problem (KP). Recent state-of-the-art TTP solvers modify the underlying TSP and KP solutions in an iterative and interleaved fashion. The TSP solution (cyclic tour) is typically changed in a deterministic way, while changes to the KP solution typically involve a random search, effectively resulting in a quasi-meandering exploration of the TTP solution space. Once a plateau is reached, the iterative search of the TTP solution space is restarted by using a new initial TSP tour. We propose to make the search more efficient through an adaptive surrogate model (based on a customised form of Support Vector Regression) that learns the characteristics of initial TSP tours that lead to good TTP solutions. The model is used to filter out non-promising initial TSP tours, in effect reducing the amount of time spent to find a good TTP solution. Experiments on a broad range of benchmark TTP instances indicate that the proposed approach filters out a considerable number of non-promising initial tours, at the cost of omitting only a small number of the best TTP solutions.

A Cooperative Coordination Solver for Travelling Thief Problems

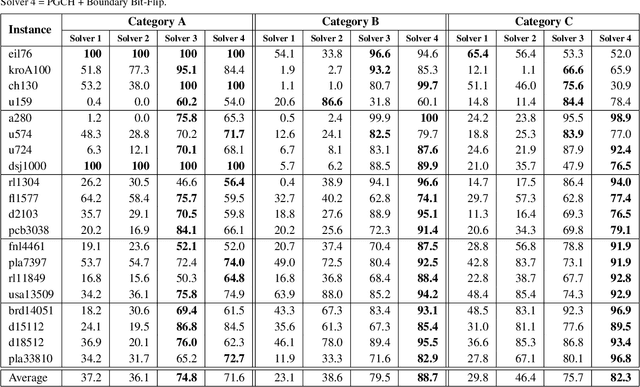
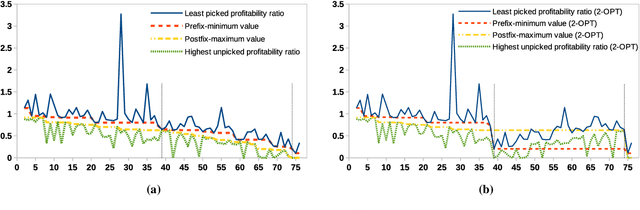
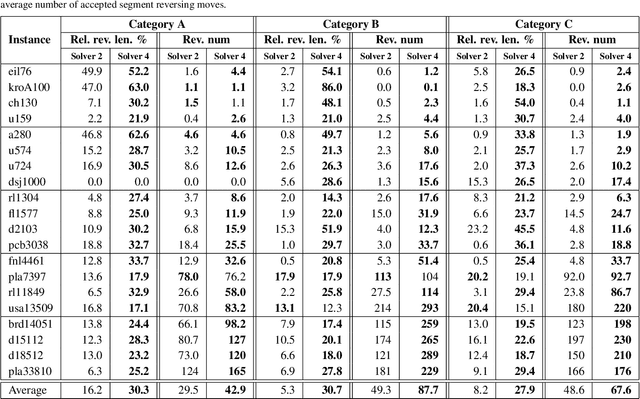
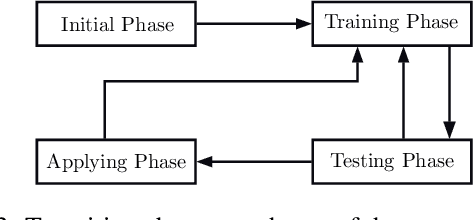
In the travelling thief problem (TTP), a thief undertakes a cyclic tour through a set of cities, and according to a picking plan, picks a subset of available items into a rented knapsack with limited capacity. The overall aim is to maximise profit while minimising renting cost. TTP combines two interdependent components: the travelling salesman problem (TSP) and the knapsack problem (KP). Existing TTP approaches typically solve the TSP and KP components in an interleaved fashion: the solution of one component is fixed while the solution of the other is changed. This indicates poor coordination between solving the two components, which may lead to poor quality TTP solutions. The 2-OPT heuristic is often used for solving the TSP component, which reverses a segment in the tour. Within the TTP context, 2-OPT does not take into account the picking plan, which can result in a lower objective value. This in turn can result in the tour modification to be rejected by a solver. To address this, we propose an extended form of 2-OPT in order to change the picking plan in coordination with modifying the tour. Items deemed as less profitable and picked in cities earlier in the reversed segment are replaced by items that tend to be equally or more profitable and not picked in cities later in the reversed segment. The picking plan is further changed through a modified form of the bit-flip search, where changes in the picking state are only permitted for boundary items, which are defined as lowest profitable picked items or highest profitable unpicked items. This restriction reduces the amount of time spent on the KP component, allowing more tours to be evaluated by the TSP component within a given time budget. The two modified heuristics form the basis of a new cooperative coordination solver, which is shown to outperform several state-of-the-art TTP solvers on a broad range of benchmark TTP instances.

Diversified Late Acceptance Search

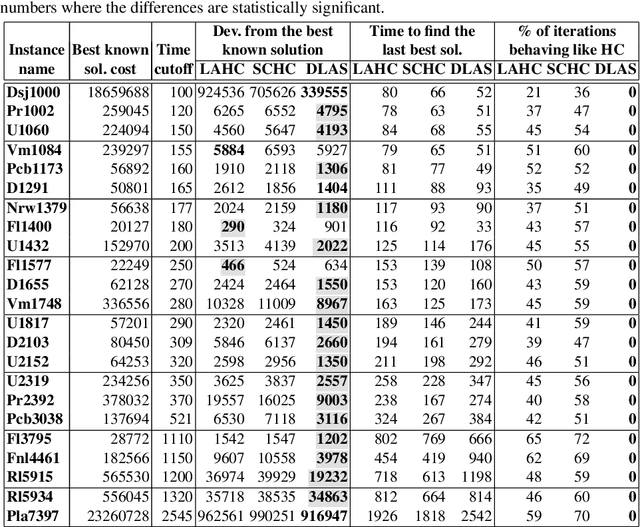
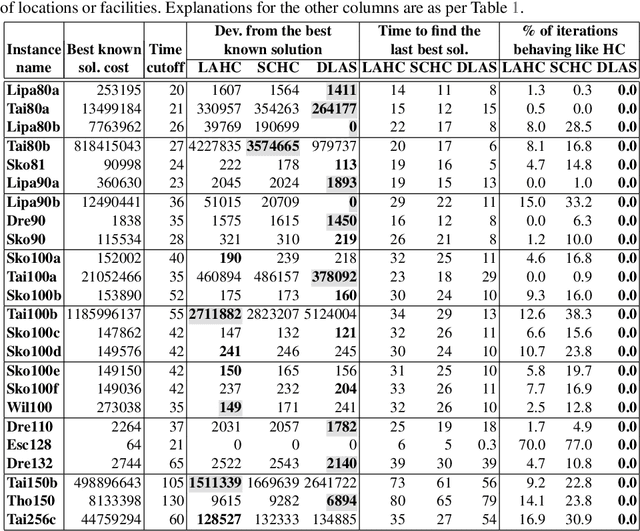
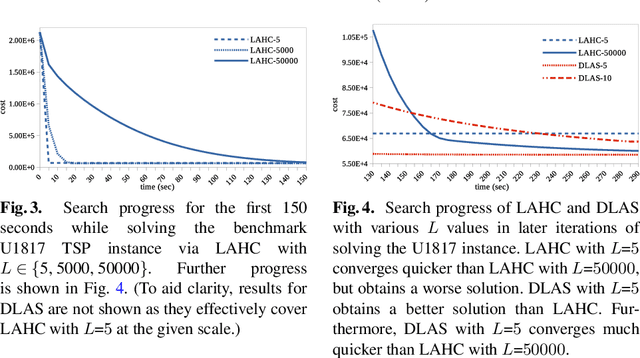
The well-known Late Acceptance Hill Climbing (LAHC) search aims to overcome the main downside of traditional Hill Climbing (HC) search, which is often quickly trapped in a local optimum due to strictly accepting only non-worsening moves within each iteration. In contrast, LAHC also accepts worsening moves, by keeping a circular array of fitness values of previously visited solutions and comparing the fitness values of candidate solutions against the least recent element in the array. While this straightforward strategy has proven effective, there are nevertheless situations where LAHC can unfortunately behave in a similar manner to HC. For example, when a new local optimum is found, often the same fitness value is stored many times in the array. To address this shortcoming, we propose new acceptance and replacement strategies to take into account worsening, improving, and sideways movement scenarios with the aim to improve the diversity of values in the array. Compared to LAHC, the proposed Diversified Late Acceptance Search approach is shown to lead to better quality solutions that are obtained with a lower number of iterations on benchmark Travelling Salesman Problems and Quadratic Assignment Problems.