Vertical Validation: Evaluating Implicit Generative Models for Graphs on Thin Support Regions

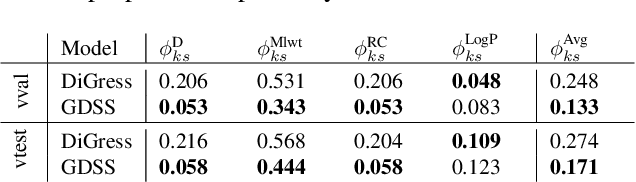
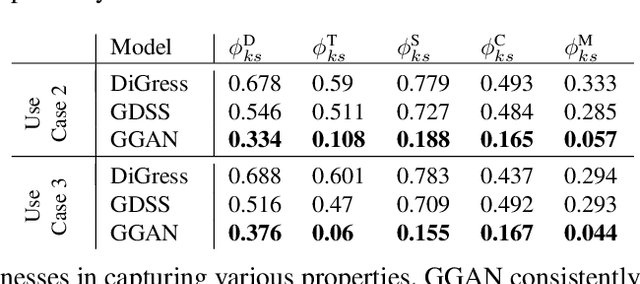
There has been a growing excitement that implicit graph generative models could be used to design or discover new molecules for medicine or material design. Because these molecules have not been discovered, they naturally lie in unexplored or scarcely supported regions of the distribution of known molecules. However, prior evaluation methods for implicit graph generative models have focused on validating statistics computed from the thick support (e.g., mean and variance of a graph property). Therefore, there is a mismatch between the goal of generating novel graphs and the evaluation methods. To address this evaluation gap, we design a novel evaluation method called Vertical Validation (VV) that systematically creates thin support regions during the train-test splitting procedure and then reweights generated samples so that they can be compared to the held-out test data. This procedure can be seen as a generalization of the standard train-test procedure except that the splits are dependent on sample features. We demonstrate that our method can be used to perform model selection if performance on thin support regions is the desired goal. As a side benefit, we also show that our approach can better detect overfitting as exemplified by memorization.

Discrete Tree Flows via Tree-Structured Permutations

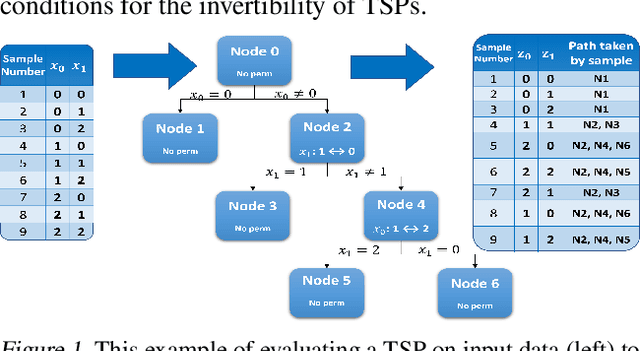
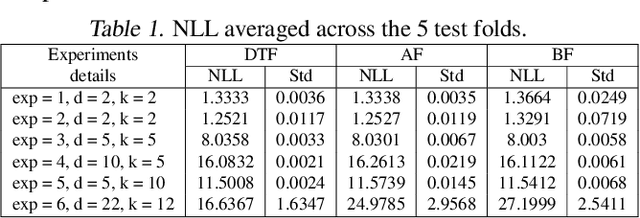
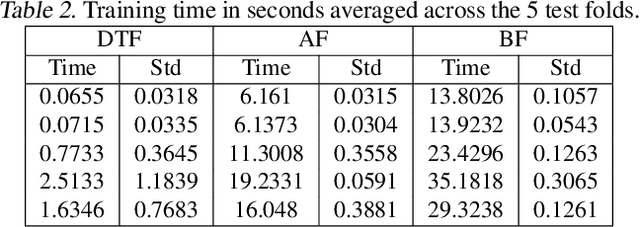
While normalizing flows for continuous data have been extensively researched, flows for discrete data have only recently been explored. These prior models, however, suffer from limitations that are distinct from those of continuous flows. Most notably, discrete flow-based models cannot be straightforwardly optimized with conventional deep learning methods because gradients of discrete functions are undefined or zero. Previous works approximate pseudo-gradients of the discrete functions but do not solve the problem on a fundamental level. In addition to that, backpropagation can be computationally burdensome compared to alternative discrete algorithms such as decision tree algorithms. Our approach seeks to reduce computational burden and remove the need for pseudo-gradients by developing a discrete flow based on decision trees -- building upon the success of efficient tree-based methods for classification and regression for discrete data. We first define a tree-structured permutation (TSP) that compactly encodes a permutation of discrete data where the inverse is easy to compute; thus, we can efficiently compute the density value and sample new data. We then propose a decision tree algorithm to build TSPs that learns the tree structure and permutations at each node via novel criteria. We empirically demonstrate the feasibility of our method on multiple datasets.