An Investigation on Machine Learning Predictive Accuracy Improvement and Uncertainty Reduction using VAE-based Data Augmentation

The confluence of ultrafast computers with large memory, rapid progress in Machine Learning (ML) algorithms, and the availability of large datasets place multiple engineering fields at the threshold of dramatic progress. However, a unique challenge in nuclear engineering is data scarcity because experimentation on nuclear systems is usually more expensive and time-consuming than most other disciplines. One potential way to resolve the data scarcity issue is deep generative learning, which uses certain ML models to learn the underlying distribution of existing data and generate synthetic samples that resemble the real data. In this way, one can significantly expand the dataset to train more accurate predictive ML models. In this study, our objective is to evaluate the effectiveness of data augmentation using variational autoencoder (VAE)-based deep generative models. We investigated whether the data augmentation leads to improved accuracy in the predictions of a deep neural network (DNN) model trained using the augmented data. Additionally, the DNN prediction uncertainties are quantified using Bayesian Neural Networks (BNN) and conformal prediction (CP) to assess the impact on predictive uncertainty reduction. To test the proposed methodology, we used TRACE simulations of steady-state void fraction data based on the NUPEC Boiling Water Reactor Full-size Fine-mesh Bundle Test (BFBT) benchmark. We found that augmenting the training dataset using VAEs has improved the DNN model's predictive accuracy, improved the prediction confidence intervals, and reduced the prediction uncertainties.

Reduced Order Modeling of a MOOSE-based Advanced Manufacturing Model with Operator Learning

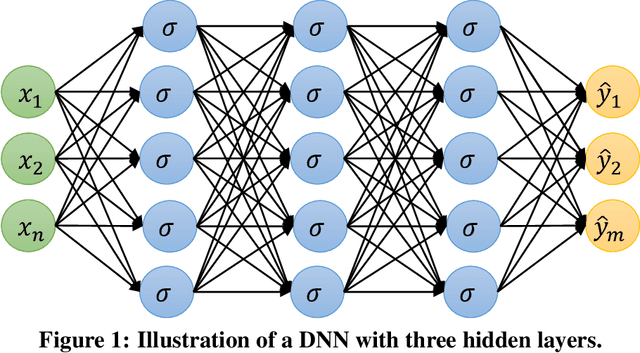
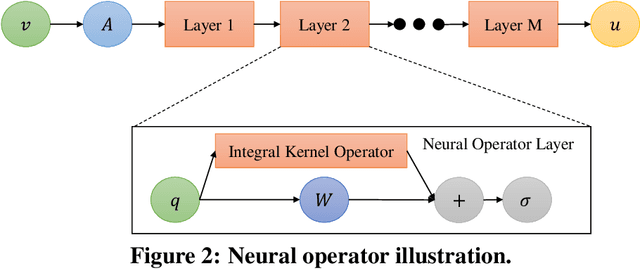
Advanced Manufacturing (AM) has gained significant interest in the nuclear community for its potential application on nuclear materials. One challenge is to obtain desired material properties via controlling the manufacturing process during runtime. Intelligent AM based on deep reinforcement learning (DRL) relies on an automated process-level control mechanism to generate optimal design variables and adaptive system settings for improved end-product properties. A high-fidelity thermo-mechanical model for direct energy deposition has recently been developed within the MOOSE framework at the Idaho National Laboratory (INL). The goal of this work is to develop an accurate and fast-running reduced order model (ROM) for this MOOSE-based AM model that can be used in a DRL-based process control and optimization method. Operator learning (OL)-based methods will be employed due to their capability to learn a family of differential equations, in this work, produced by changing process variables in the Gaussian point heat source for the laser. We will develop OL-based ROM using Fourier neural operator, and perform a benchmark comparison of its performance with a conventional deep neural network-based ROM.

Fast and Accurate Reduced-Order Modeling of a MOOSE-based Additive Manufacturing Model with Operator Learning

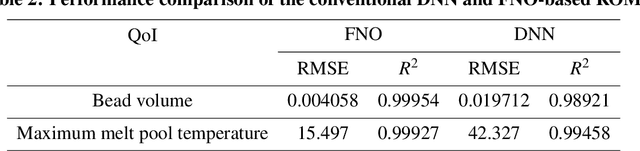
One predominant challenge in additive manufacturing (AM) is to achieve specific material properties by manipulating manufacturing process parameters during the runtime. Such manipulation tends to increase the computational load imposed on existing simulation tools employed in AM. The goal of the present work is to construct a fast and accurate reduced-order model (ROM) for an AM model developed within the Multiphysics Object-Oriented Simulation Environment (MOOSE) framework, ultimately reducing the time/cost of AM control and optimization processes. Our adoption of the operator learning (OL) approach enabled us to learn a family of differential equations produced by altering process variables in the laser's Gaussian point heat source. More specifically, we used the Fourier neural operator (FNO) and deep operator network (DeepONet) to develop ROMs for time-dependent responses. Furthermore, we benchmarked the performance of these OL methods against a conventional deep neural network (DNN)-based ROM. Ultimately, we found that OL methods offer comparable performance and, in terms of accuracy and generalizability, even outperform DNN at predicting scalar model responses. The DNN-based ROM afforded the fastest training time. Furthermore, all the ROMs were faster than the original MOOSE model yet still provided accurate predictions. FNO had a smaller mean prediction error than DeepONet, with a larger variance for time-dependent responses. Unlike DNN, both FNO and DeepONet were able to simulate time series data without the need for dimensionality reduction techniques. The present work can help facilitate the AM optimization process by enabling faster execution of simulation tools while still preserving evaluation accuracy.

Functional PCA and Deep Neural Networks-based Bayesian Inverse Uncertainty Quantification with Transient Experimental Data

Inverse UQ is the process to inversely quantify the model input uncertainties based on experimental data. This work focuses on developing an inverse UQ process for time-dependent responses, using dimensionality reduction by functional principal component analysis (PCA) and deep neural network (DNN)-based surrogate models. The demonstration is based on the inverse UQ of TRACE physical model parameters using the FEBA transient experimental data. The measurement data is time-dependent peak cladding temperature (PCT). Since the quantity-of-interest (QoI) is time-dependent that corresponds to infinite-dimensional responses, PCA is used to reduce the QoI dimension while preserving the transient profile of the PCT, in order to make the inverse UQ process more efficient. However, conventional PCA applied directly to the PCT time series profiles can hardly represent the data precisely due to the sudden temperature drop at the time of quenching. As a result, a functional alignment method is used to separate the phase and amplitude information of the transient PCT profiles before dimensionality reduction. DNNs are then trained using PC scores from functional PCA to build surrogate models of TRACE in order to reduce the computational cost in Markov Chain Monte Carlo sampling. Bayesian neural networks are used to estimate the uncertainties of DNN surrogate model predictions. In this study, we compared four different inverse UQ processes with different dimensionality reduction methods and surrogate models. The proposed approach shows an improvement in reducing the dimension of the TRACE transient simulations, and the forward propagation of inverse UQ results has a better agreement with the experimental data.

Quantification of Deep Neural Network Prediction Uncertainties for VVUQ of Machine Learning Models

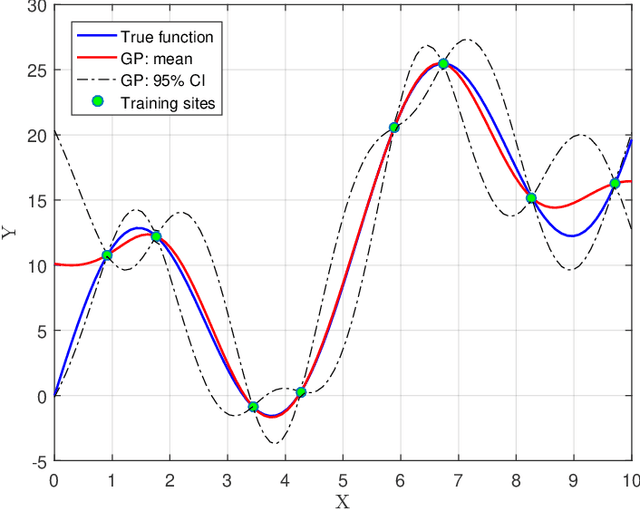
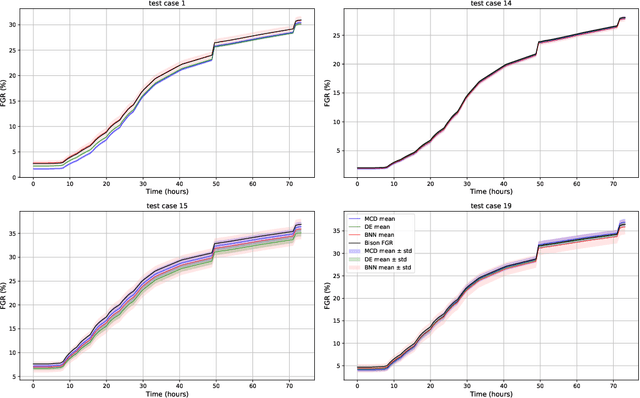
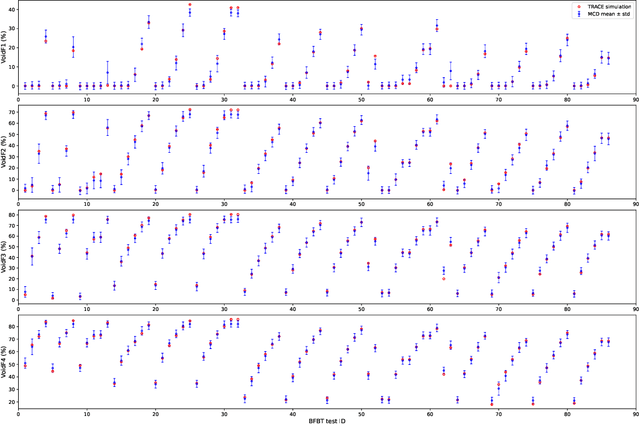
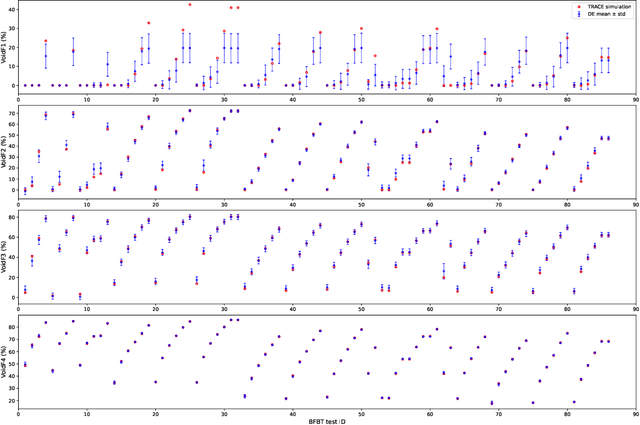
Recent performance breakthroughs in Artificial intelligence (AI) and Machine learning (ML), especially advances in Deep learning (DL), the availability of powerful, easy-to-use ML libraries (e.g., scikit-learn, TensorFlow, PyTorch.), and increasing computational power have led to unprecedented interest in AI/ML among nuclear engineers. For physics-based computational models, Verification, Validation and Uncertainty Quantification (VVUQ) have been very widely investigated and a lot of methodologies have been developed. However, VVUQ of ML models has been relatively less studied, especially in nuclear engineering. In this work, we focus on UQ of ML models as a preliminary step of ML VVUQ, more specifically, Deep Neural Networks (DNNs) because they are the most widely used supervised ML algorithm for both regression and classification tasks. This work aims at quantifying the prediction, or approximation uncertainties of DNNs when they are used as surrogate models for expensive physical models. Three techniques for UQ of DNNs are compared, namely Monte Carlo Dropout (MCD), Deep Ensembles (DE) and Bayesian Neural Networks (BNNs). Two nuclear engineering examples are used to benchmark these methods, (1) time-dependent fission gas release data using the Bison code, and (2) void fraction simulation based on the BFBT benchmark using the TRACE code. It was found that the three methods typically require different DNN architectures and hyperparameters to optimize their performance. The UQ results also depend on the amount of training data available and the nature of the data. Overall, all these three methods can provide reasonable estimations of the approximation uncertainties. The uncertainties are generally smaller when the mean predictions are close to the test data, while the BNN methods usually produce larger uncertainties than MCD and DE.