Mahmoud Aldababsa
STAR-RIS-Aided Secure Communications:Analytical Insights and Performance Comparison
Dec 12, 2025Abstract:Simultaneously transmitting and reflecting reconfigurable intelligent surfaces (STAR-RISs) have emerged as a promising technology for enabling full-space signal manipulation and enhancing wireless network coverage and capacity. In this article, we present a comprehensive analytical comparison of STAR-RIS-assisted systems with single-input single-output (SISO), conventional RISs, and decode-and-forward (DF) relaying schemes, including both half-duplex (HD) and full-duplex (FD) modes. Closed-form expressions are derived for the achievable secrecy rates of STAR-RIS-aided communications under both the absence and presence of eavesdroppers. Unlike most existing works, the direct source destination link is incorporated in all considered schemes, and optimal transmit power allocation is investigated for HD and FD-DF relaying. Furthermore, we provide the conditions under which STAR-RIS outperforms HD- and FD-DF relaying and quantify the minimum number of STAR-RIS elements required to achieve superior rates. The impacts of key system parameters including transmit power, number of elements, reflection-to-transmission power ratio, element-splitting factor, and deployment positions on both achievable and secrecy performance are investigated. The results reveal that STAR-RIS systems can achieve superior rates and secrecy rates compared to all benchmark schemes.
Novel Selection Schemes for Multi-RIS-Assisted Fluid Antenna Systems
Apr 28, 2025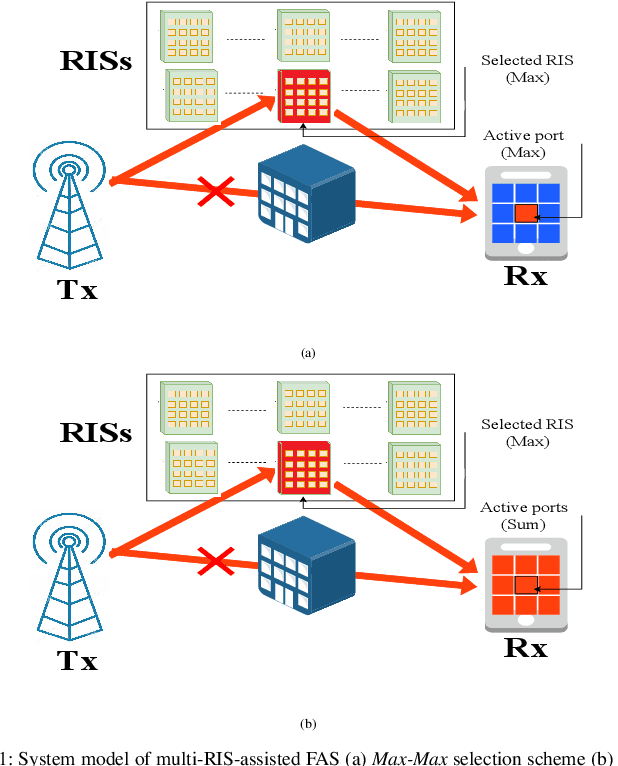
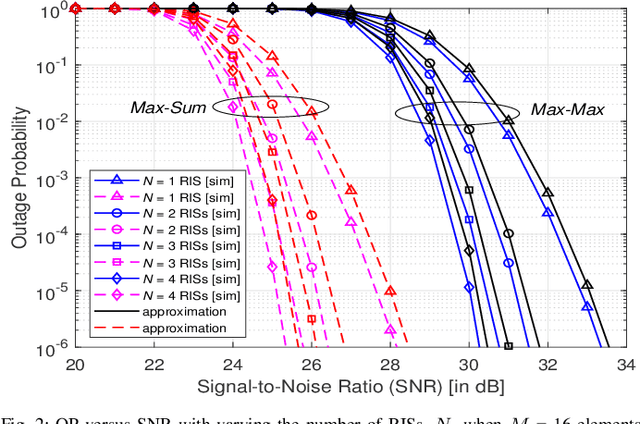
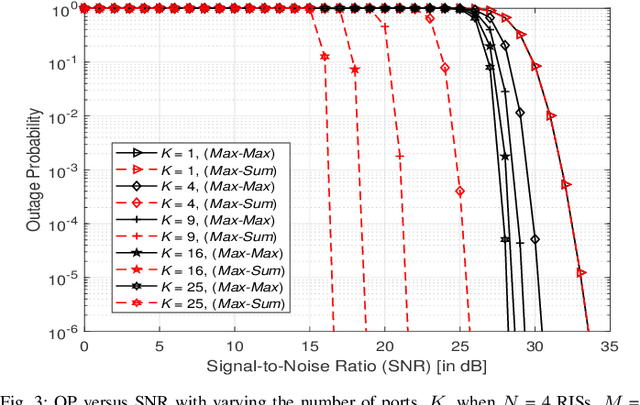
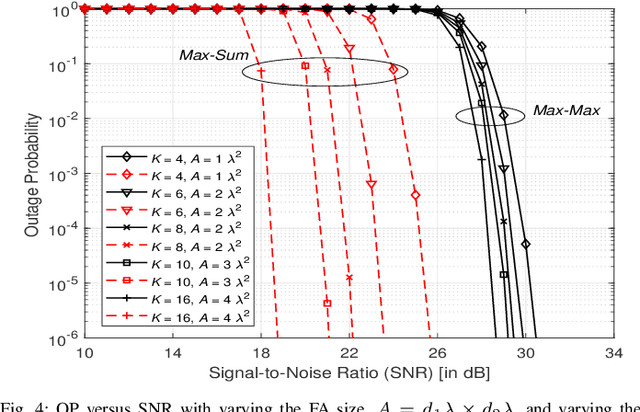
Abstract:This paper investigates the performance of a multi-reconfigurable intelligent surface (RIS)-assisted fluid antenna system (FAS). In this system, a single-antenna transmitter communicates with a receiver equipped with a planar FAS through multiple RISs in the absence of a direct link. To enhance the system performance, we propose two novel selection schemes: \textit{Max-Max} and \textit{Max-Sum}. In particular, the \textit{Max-Max} scheme selects the best combination of a single RIS and a single fluid antenna (FA) port that offers the maximum signal-to-noise ratio (SNR) at the receiver. On the other hand, the \textit{Max-Sum} scheme selects one RIS while activating all FA ports providing the highest overall SNR. We conduct a detailed performance analysis of the proposed system under Nakagami-$m$ fading channels. First, we derive the cumulative distribution function (CDF) of the SNR for both selection schemes. The derived CDF is then used to obtain approximate theoretical expressions for the outage probability (OP) and the delay outage rate (DOR). Next, a high-SNR asymptotic analysis is carried out to provide further insights into the system performance in terms of diversity and coding gains. Finally, the analytical results are validated through extensive Monte Carlo simulations, demonstrating their accuracy and providing a comprehensive understanding of the system's performance.
Multiple RISs-Aided Networks: Performance Analysis and Optimization
Jun 11, 2022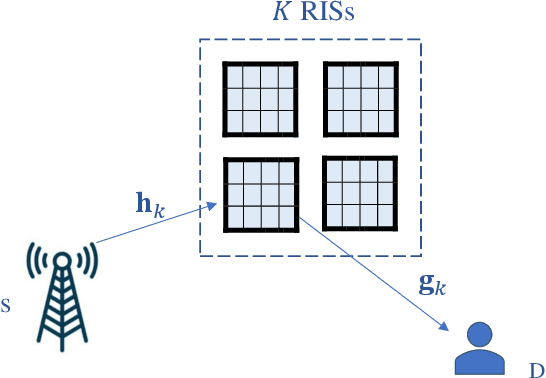
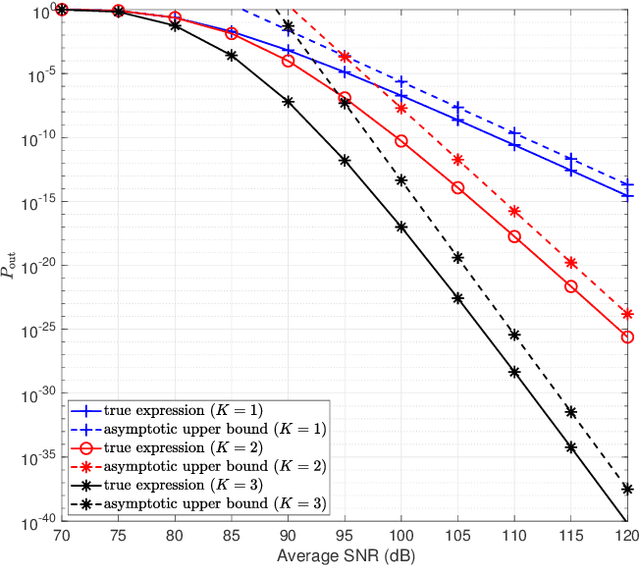
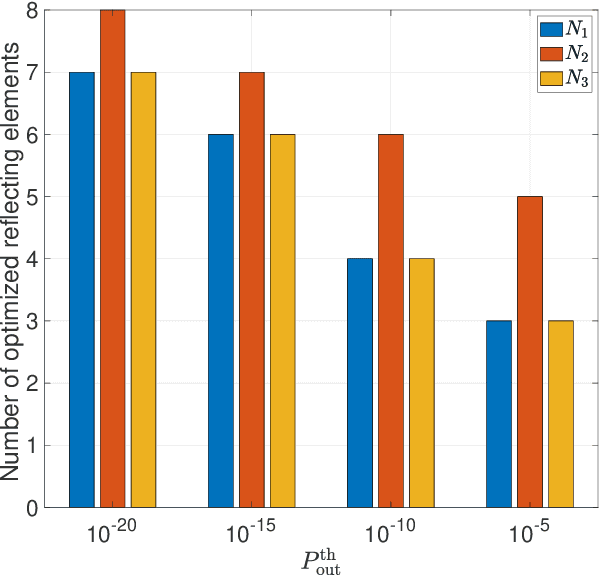
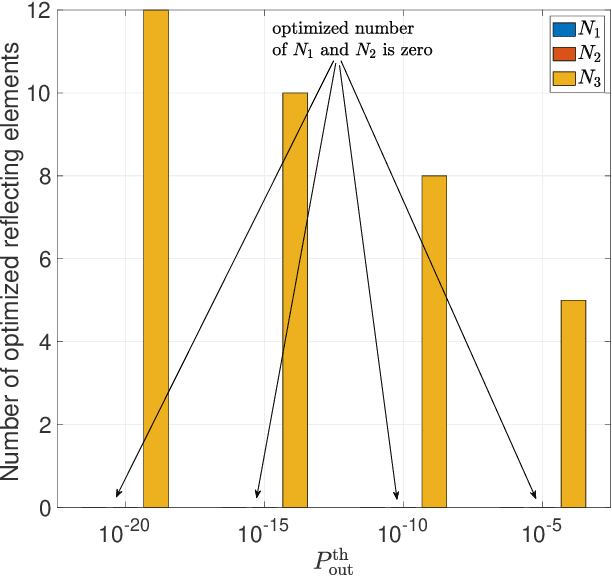
Abstract:This paper analyzes the performance of multiple reconfigurable intelligent surfaces (RISs)-aided networks. The paper also provides some optimization results on the number of reflecting elements on RISs and the optimal placement of RISs. We first derive accurate closed-form approximations for RIS channels' distributions assuming independent non-identically distributed (i.ni.d.) Nakagami-\emph{m} fading environment. Then, the approximate expressions for outage probability (OP) and average symbol error probability are derived in closed-form. Furthermore, to get more insights into the system performance, we derive the asymptotic OP at the high signal-to-noise ratio regime and provide closed-form expressions for the system diversity order and coding gain. Finally, the accuracy of our theoretical analysis is validated through Monte-Carlo simulations. The obtained results show that the considered RIS scenario can provide a diversity order of $\frac{a}{2}K$, where $a$ is a function of the Nakagami fading parameter $m$ and the number of meta-surface elements $N$, and $K$ is the number of RISs.
STAR-RIS-NOMA Networks: An Error Performance Perspective
Feb 19, 2022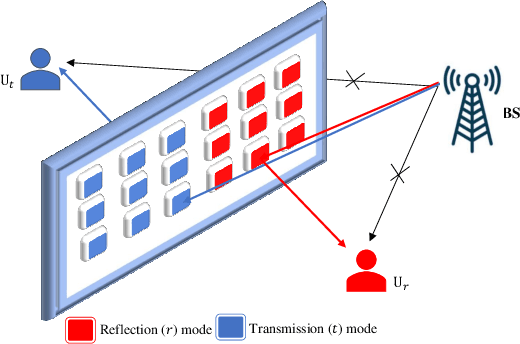
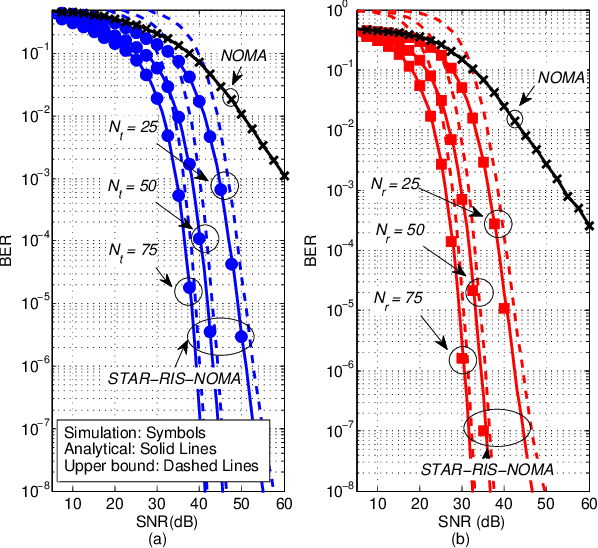
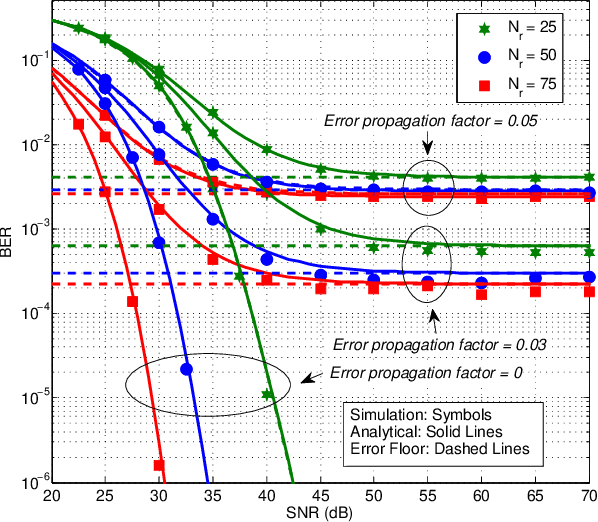

Abstract:This letter investigates the bit error rate (BER) performance of simultaneous transmitting and reflecting reconfigurable intelligent surfaces (STAR-RISs) in non-orthogonal multiple access (NOMA) networks. In the investigated network, a STAR-RIS serves two non-orthogonal users located on either side of the surface by utilizing the mode switching protocol. We derive the closed-form and upper bound BER expressions in perfect and imperfect successive interference cancellation cases. Furthermore, asymptotic analyses are also conducted to provide further insights into the BER behavior in the high signal-to-noise ratio region. Finally, the accuracy of our theoretical analysis is validated through Monte Carlo simulations. The obtained results reveal that the BER performance of STAR-RIS-NOMA outperforms that of the classical NOMA system, and STAR-RIS might be a promising NOMA 2.0 solution.
Simultaneous Transmitting and ReflectingIntelligent Surfaces-Empowered NOMA Networks
Oct 11, 2021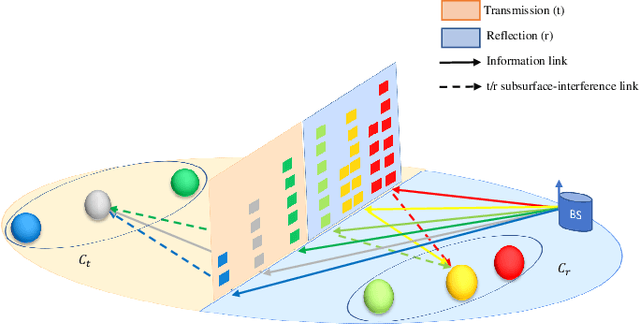
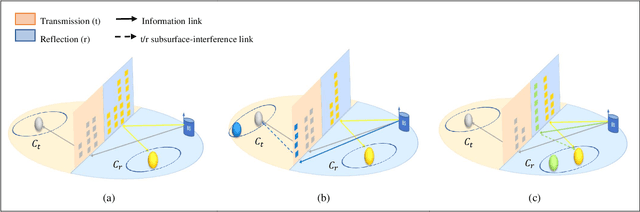
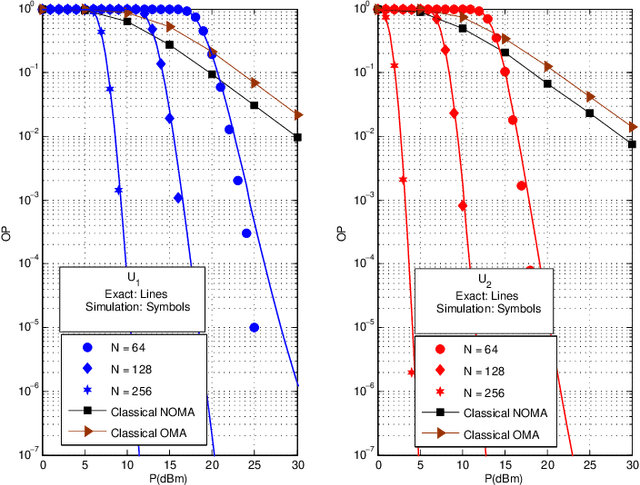
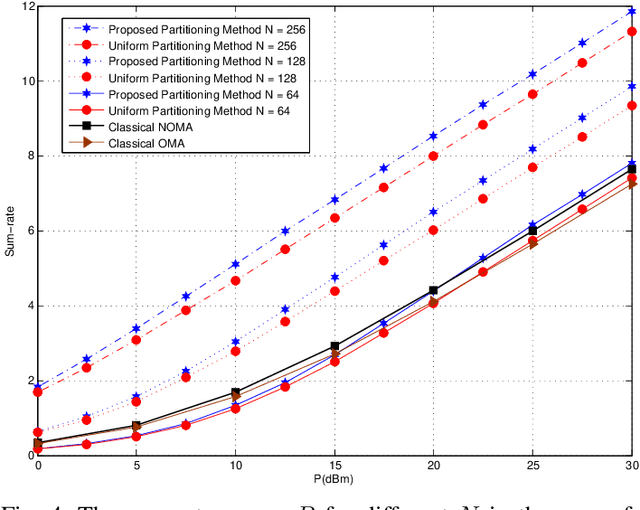
Abstract:In this paper, we propose simultaneous transmitting and reflecting reconfigurable intelligent surface (STAR-RIS) assisted non-orthogonal multiple access (NOMA) networks. The considered STAR-RIS utilizes the mode switching (MS) protocol to serve multiple NOMA users located on both sides of the RIS surface. Based on the MS protocol, each STAR-RIS element can operate in full transmission or reflection mode. Within this perspective, we propose a novel algorithm to partition the STAR-RIS surface among the available users. This algorithm aims to determine the proper number of transmitting/reflecting elements needs to be assigned to each user in order to maximize the system sum-rate while guaranteeing the quality-of-service requirements for individual users. For the proposed system, we derive closed-form analytical expressions for the outage probability (OP) and its corresponding asymptotic behavior under different user deployments. Finally, Monte Carlo simulations are performed in order to verify the correctness of the theoretical analysis. It is shown that the proposed system outperforms the classical NOMA and orthogonal multiple access systems in terms of OP and sum-rate.
Joint Transmit and Receive Antenna Selection System for MIMO-NOMA with Energy Harvesting
Apr 25, 2021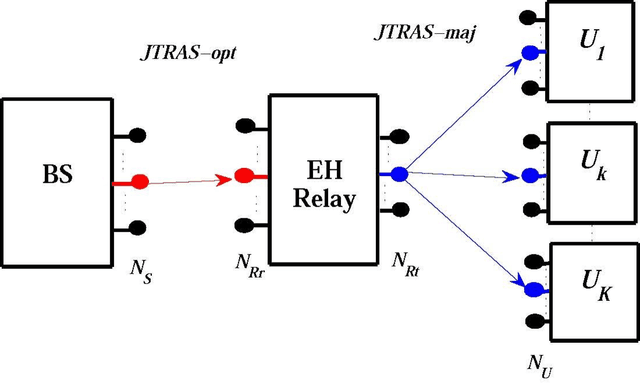
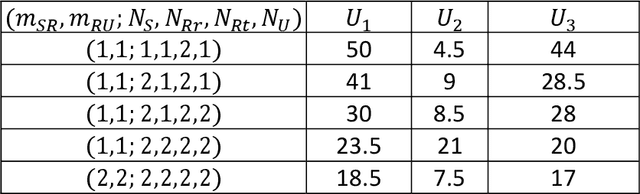
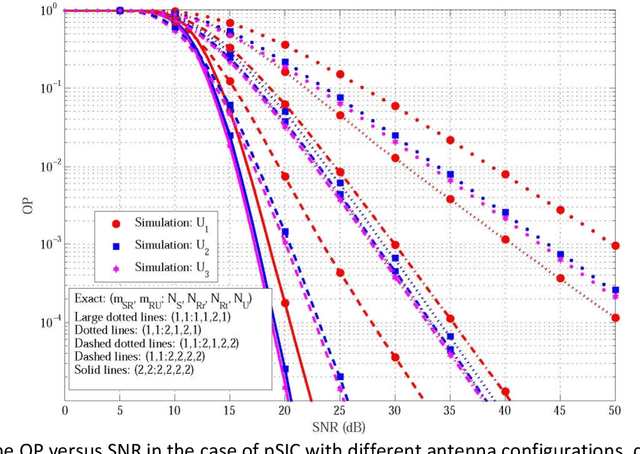
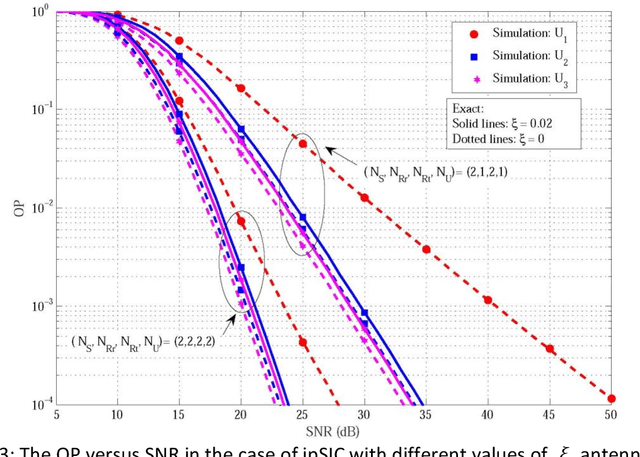
Abstract:In this paper, outage probability (OP) of a joint transmit and receive antenna selection (JTRAS) scheme is analyzed in multiple-input multiple-output non orthogonal multiple access based downlink energy harvesting (EH) relaying networks. In this dual-hop and amplify-and-forward relaying based network, since the first and second hops are types of single-user and multi-user systems, respectively, the optimal JTRAS and suboptimal majority-based JTRAS schemes are employed in the first and second hops. The theoretical OP analysis is carried out over Nakagami-m fading channels in the cases of perfect and imperfect successive interference cancellation. Finally, Monte Carlo simulations are performed to substantiate the accuracy of the theoretical analysis. It is shown that the optimal power splitting ratios at the EH relay are different for users and the users with good channel conditions have minimum optimal ratios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge