Finite Blocklength Secrecy Analysis of Polar and Reed-Muller Codes in BEC Semi-Deterministic Wiretap Channels

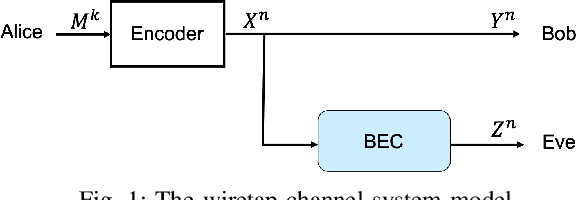
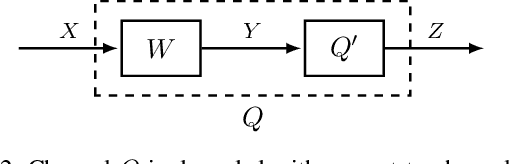
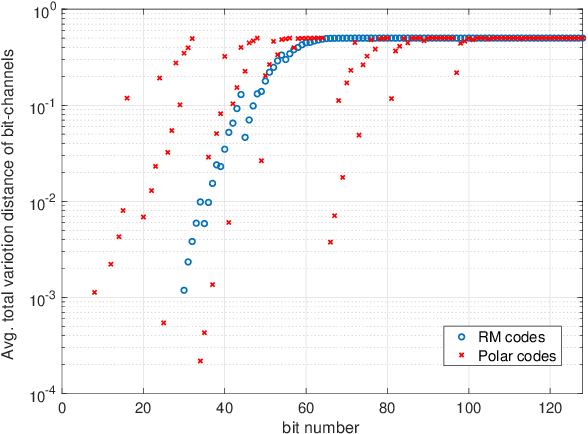
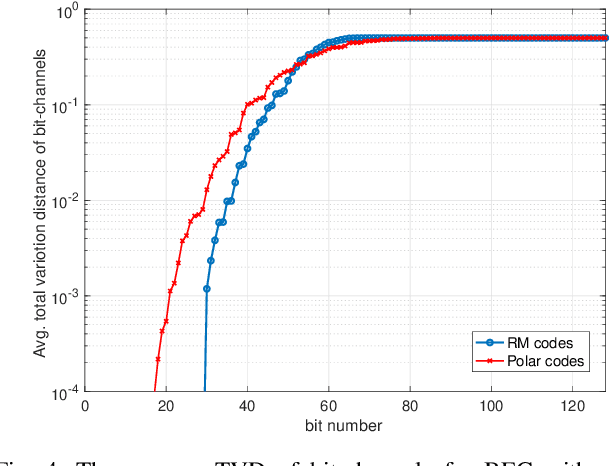
In this paper, we consider a semi-deterministic wiretap channel where the main channel is noiseless and the eavesdropper's channel is a binary erasure channel (BEC). We provide a lower bound for the achievable secrecy rates of polar and Reed Muller codes and compare it to the second order coding rate for the semi-deterministic wiretap channel. To the best of our knowledge, this is the first work which demonstrates the secrecy performance of polar and Reed-Muller codes in short blocklengths. The results show that under a total variation secrecy metric, Reed Muller codes can achieve secrecy rates very close to the second order approximation rate. On the other hand, we observe a significant gap between the lower bound for the achievable rates of polar codes and the the second order approximation rate for short blocklengths.

Comparison of Short Blocklength Slepian-Wolf Coding for Key Reconciliation

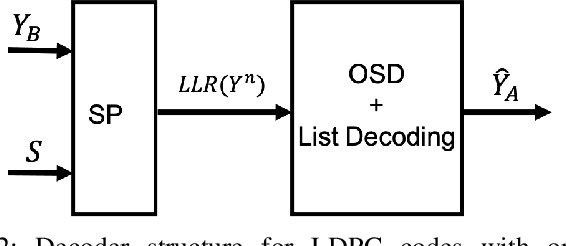
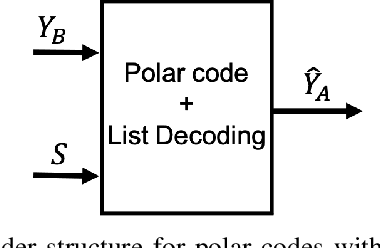
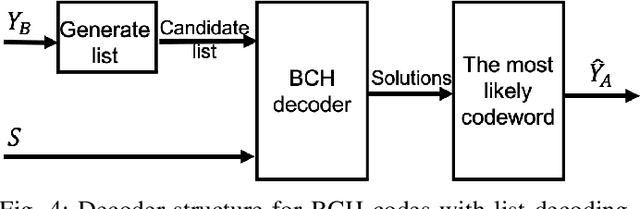
We focus Slepian-Wolf (SW) coding in the short blocklength for reconciliation in secret key generation and physical unclonable functions. In the problem formulation, two legitimate parties wish to generate a common secret key from a noisy observation of a common random source in the presence of a passive eavesdropper. We consider three different families of codes for key reconciliation. The selected codes show promising performances in information transmission in the short block-length regime. We implement and compare the performance of different codes for SW reconciliation in the terms of reliability and decoding complexity.