Maen Alzubi
Fuzzy Rule Interpolation Toolbox for the GNU Open-Source OCTAVE
Dec 10, 2019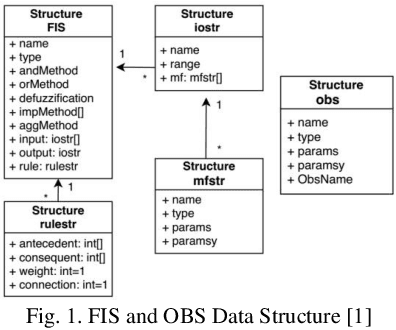
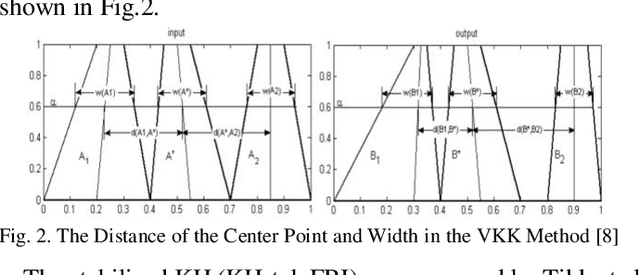
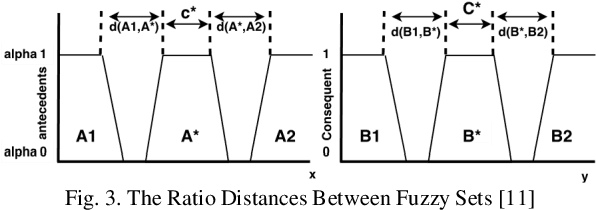
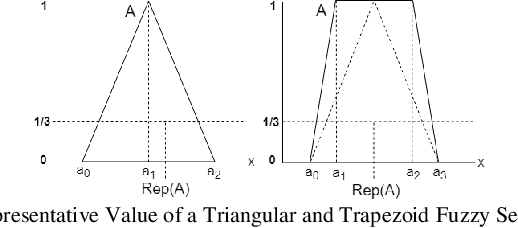
Abstract:In most fuzzy control applications (applying classical fuzzy reasoning), the reasoning method requires a complete fuzzy rule-base, i.e all the possible observations must be covered by the antecedents of the fuzzy rules, which is not always available. Fuzzy control systems based on the Fuzzy Rule Interpolation (FRI) concept play a major role in different platforms, in case if only a sparse fuzzy rule-base is available. This cases the fuzzy model contains only the most relevant rules, without covering all the antecedent universes. The first FRI toolbox being able to handle different FRI methods was developed by Johanyak et. al. in 2006 for the MATLAB environment. The goal of this paper is to introduce some details of the adaptation of the FRI toolbox to support the GNU/OCTAVE programming language. The OCTAVE Fuzzy Rule Interpolation (OCTFRI) Toolbox is an open-source toolbox for OCTAVE programming language, providing a large functionally compatible subset of the MATLAB FRI toolbox as well as many extensions. The OCTFRI Toolbox includes functions that enable the user to evaluate Fuzzy Inference Systems (FISs) from the command line and from OCTAVE scripts, read/write FISs and OBS to/from files, and produce a graphical visualisation of both the membership functions and the FIS outputs. Future work will focus on implementing advanced fuzzy inference techniques and GUI tools.
Some Considerations and a Benchmark Related to the CNF Property of the Koczy-Hirota Fuzzy Rule Interpolation
Nov 12, 2019



Abstract:The goal of this paper is twofold. Once to highlight some basic problematic properties of the KH Fuzzy Rule Interpolation through examples, secondly to set up a brief Benchmark set of Examples, which is suitable for testing other Fuzzy Rule Interpolation (FRI) methods against these ill conditions. Fuzzy Rule Interpolation methods were originally proposed to handle the situation of missing fuzzy rules (sparse rule-bases) and to reduce the decision complexity. Fuzzy Rule Interpolation is an important technique for implementing inference with sparse fuzzy rule-bases. Even if a given observation has no overlap with the antecedent of any rule from the rule-base, FRI may still conclude a conclusion. The first FRI method was the Koczy and Hirota proposed "Linear Interpolation", which was later renamed to "KH Fuzzy Interpolation" by the followers. There are several conditions and criteria have been suggested for unifying the common requirements an FRI methods have to satisfy. One of the most common one is the demand for a convex and normal fuzzy (CNF) conclusion, if all the rule antecedents and consequents are CNF sets. The KH FRI is the one, which cannot fulfill this condition. This paper is focusing on the conditions, where the KH FRI fails the demand for the CNF conclusion. By setting up some CNF rule examples, the paper also defines a Benchmark, in which other FRI methods can be tested if they can produce CNF conclusion where the KH FRI fails.
Investigating The Piece-Wise Linearity And Benchmark Related To Koczy-Hirota Fuzzy Linear Interpolation
Jul 01, 2019



Abstract:Fuzzy Rule Interpolation (FRI) reasoning methods have been introduced to address sparse fuzzy rule bases and reduce complexity. The first FRI method was the Koczy and Hirota (KH) proposed "Linear Interpolation". Besides, several conditions and criteria have been suggested for unifying the common requirements FRI methods have to satisfy. One of the most conditions is restricted the fuzzy set of the conclusion must preserve a Piece-Wise Linearity (PWL) if all antecedents and consequents of the fuzzy rules are preserving on PWL sets at {\alpha}-cut levels. The KH FRI is one of FRI methods which cannot satisfy this condition. Therefore, the goal of this paper is to investigate equations and notations related to PWL property, which is aimed to highlight the problematic properties of the KH FRI method to prove its efficiency with PWL condition. In addition, this paper is focusing on constructing benchmark examples to be a baseline for testing other FRI methods against situations that are not satisfied with the linearity condition for KH FRI.
Fuzzy Rule Interpolation Methods and Fri Toolbox
Apr 27, 2019



Abstract:FRI methods are less popular in the practical application domain. One possible reason is the missing common framework. There are many FRI methods developed independently, having different interpolation concepts and features. One trial for setting up a common FRI framework was the MATLAB FRI Toolbox, developed by Johany\'ak et. al. in 2006. The goals of this paper are divided as follows: firstly, to present a brief introduction of the FRI methods. Secondly, to introduce a brief description of the refreshed and extended version of the original FRI Toolbox. And thirdly, to use different unified numerical benchmark examples to evaluate and analyze the Fuzzy Rule Interpolation Techniques (FRI) (KH, KH Stabilized, MACI, IMUL, CRF, VKK, GM, FRIPOC, LESFRI, and SCALEMOVE), that will be classified and compared based on different features by following the abnormality and linearity conditions [15].
Evaluation of Machine Learning Algorithms for Intrusion Detection System
Jan 08, 2018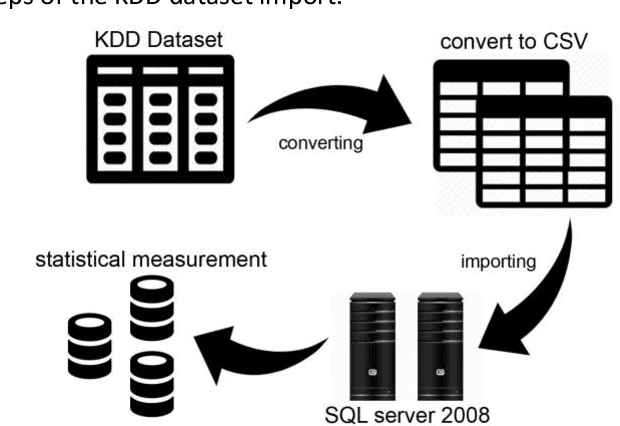
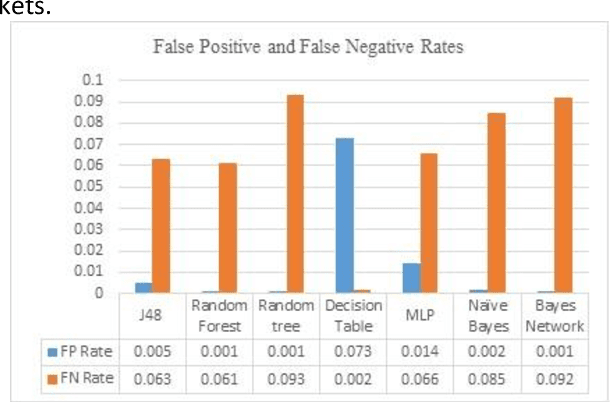
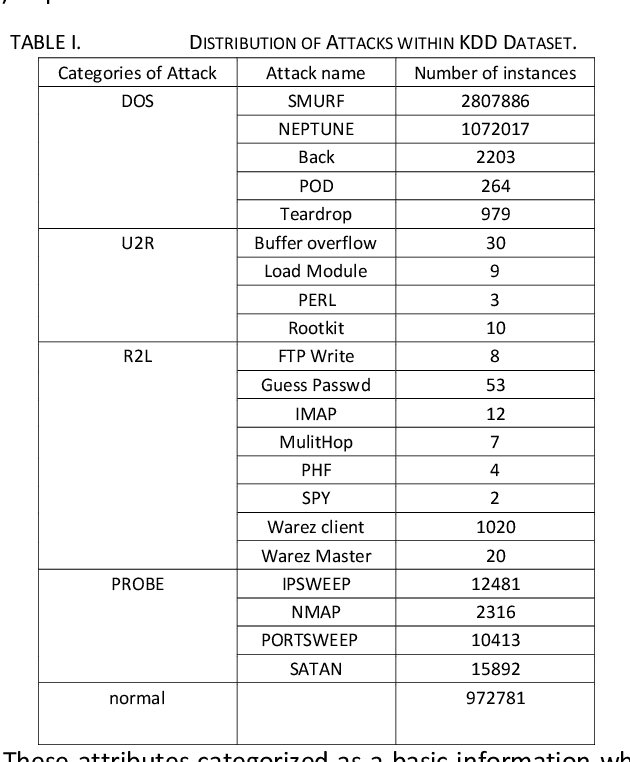
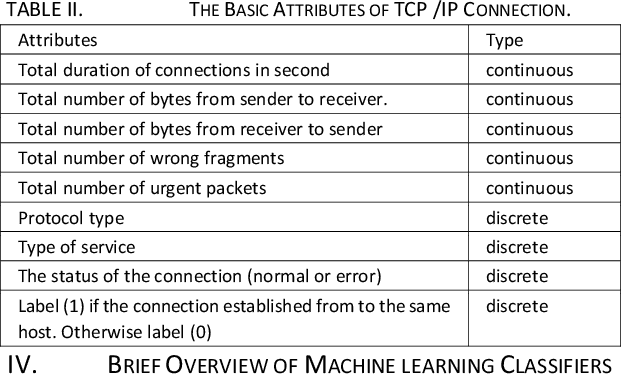
Abstract:Intrusion detection system (IDS) is one of the implemented solutions against harmful attacks. Furthermore, attackers always keep changing their tools and techniques. However, implementing an accepted IDS system is also a challenging task. In this paper, several experiments have been performed and evaluated to assess various machine learning classifiers based on KDD intrusion dataset. It succeeded to compute several performance metrics in order to evaluate the selected classifiers. The focus was on false negative and false positive performance metrics in order to enhance the detection rate of the intrusion detection system. The implemented experiments demonstrated that the decision table classifier achieved the lowest value of false negative while the random forest classifier has achieved the highest average accuracy rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge