Neural models for prediction of spatially patterned phase transitions: methods and challenges

Dryland vegetation ecosystems are known to be susceptible to critical transitions between alternative stable states when subjected to external forcing. Such transitions are often discussed through the framework of bifurcation theory, but the spatial patterning of vegetation, which is characteristic of drylands, leads to dynamics that are much more complex and diverse than local bifurcations. Recent methodological developments in Early Warning Signal (EWS) detection have shown promise in identifying dynamical signatures of oncoming critical transitions, with particularly strong predictive capabilities being demonstrated by deep neural networks. However, a machine learning model trained on synthetic examples is only useful if it can effectively transfer to a test case of practical interest. These models' capacity to generalize in this manner has been demonstrated for bifurcation transitions, but it is not as well characterized for high-dimensional phase transitions. This paper explores the successes and shortcomings of neural EWS detection for spatially patterned phase transitions, and shows how these models can be used to gain insight into where and how EWS-relevant information is encoded in spatiotemporal dynamics. A few paradigmatic test systems are used to illustrate how the capabilities of such models can be probed in a number of ways, with particular attention to the performances of a number of proposed statistical indicators for EWS and to the supplementary task of distinguishing between abrupt and continuous transitions. Results reveal that model performance often changes dramatically when training and test data sources are interchanged, which offers new insight into the criteria for model generalization.

Predicting discrete-time bifurcations with deep learning

Many natural and man-made systems are prone to critical transitions -- abrupt and potentially devastating changes in dynamics. Deep learning classifiers can provide an early warning signal (EWS) for critical transitions by learning generic features of bifurcations (dynamical instabilities) from large simulated training data sets. So far, classifiers have only been trained to predict continuous-time bifurcations, ignoring rich dynamics unique to discrete-time bifurcations. Here, we train a deep learning classifier to provide an EWS for the five local discrete-time bifurcations of codimension-1. We test the classifier on simulation data from discrete-time models used in physiology, economics and ecology, as well as experimental data of spontaneously beating chick-heart aggregates that undergo a period-doubling bifurcation. The classifier outperforms commonly used EWS under a wide range of noise intensities and rates of approach to the bifurcation. It also predicts the correct bifurcation in most cases, with particularly high accuracy for the period-doubling, Neimark-Sacker and fold bifurcations. Deep learning as a tool for bifurcation prediction is still in its nascence and has the potential to transform the way we monitor systems for critical transitions.

Universal Early Warning Signals of Phase Transitions in Climate Systems

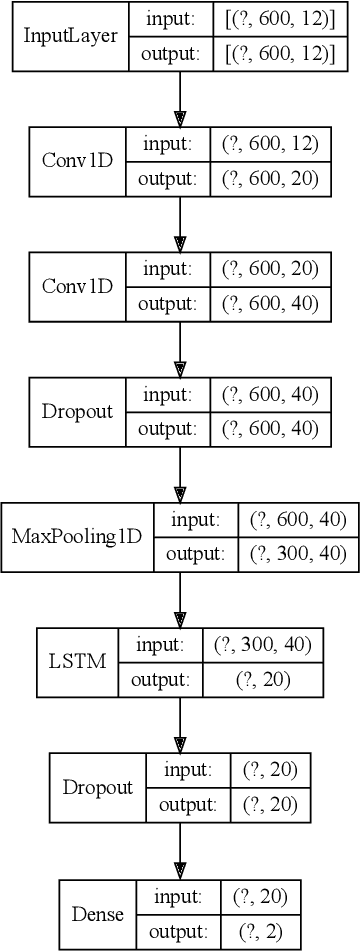
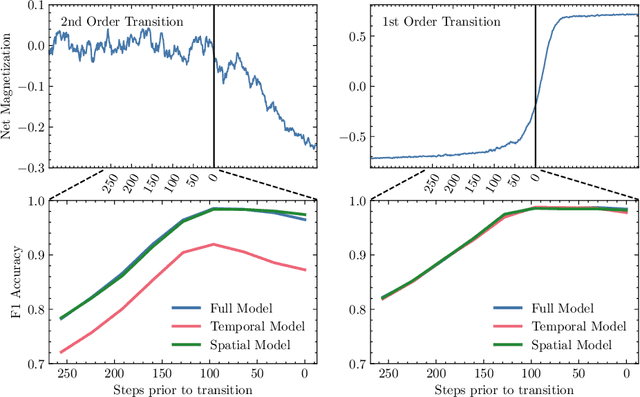
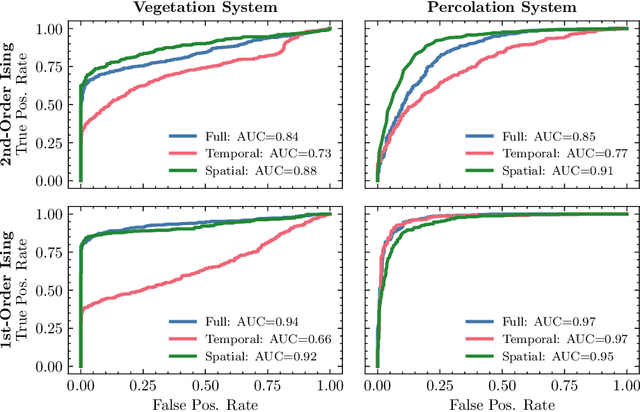
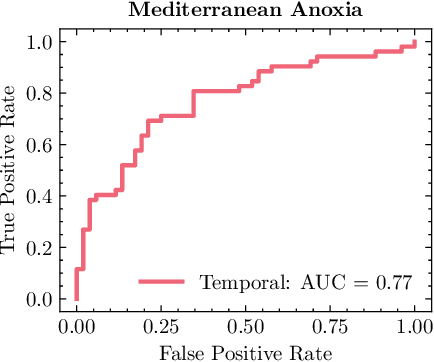
The potential for complex systems to exhibit tipping points in which an equilibrium state undergoes a sudden and potentially irreversible shift is well established, but prediction of these events using standard forecast modeling techniques is quite difficult. This has led to the development of an alternative suite of methods that seek to identify signatures of critical phenomena in data, which are expected to occur in advance of many classes of dynamical bifurcation. Crucially, the manifestations of these critical phenomena are generic across a variety of systems, meaning that data-intensive deep learning methods can be trained on (abundant) synthetic data and plausibly prove effective when transferred to (more limited) empirical data sets. This paper provides a proof of concept for this approach as applied to lattice phase transitions: a deep neural network trained exclusively on 2D Ising model phase transitions is tested on a number of real and simulated climate systems with considerable success. Its accuracy frequently surpasses that of conventional statistical indicators, with performance shown to be consistently improved by the inclusion of spatial indicators. Tools such as this may offer valuable insight into climate tipping events, as remote sensing measurements provide increasingly abundant data on complex geospatially-resolved Earth systems.