Madhav Achar
Global Unifying Intrinsic Calibration for Spinning and Solid-State LiDARs
Dec 06, 2020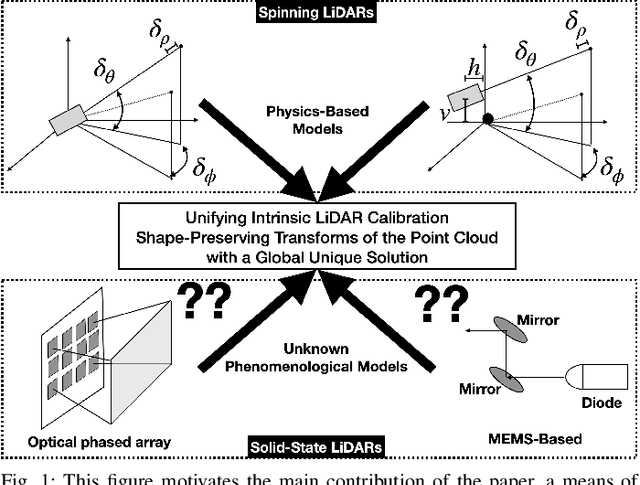
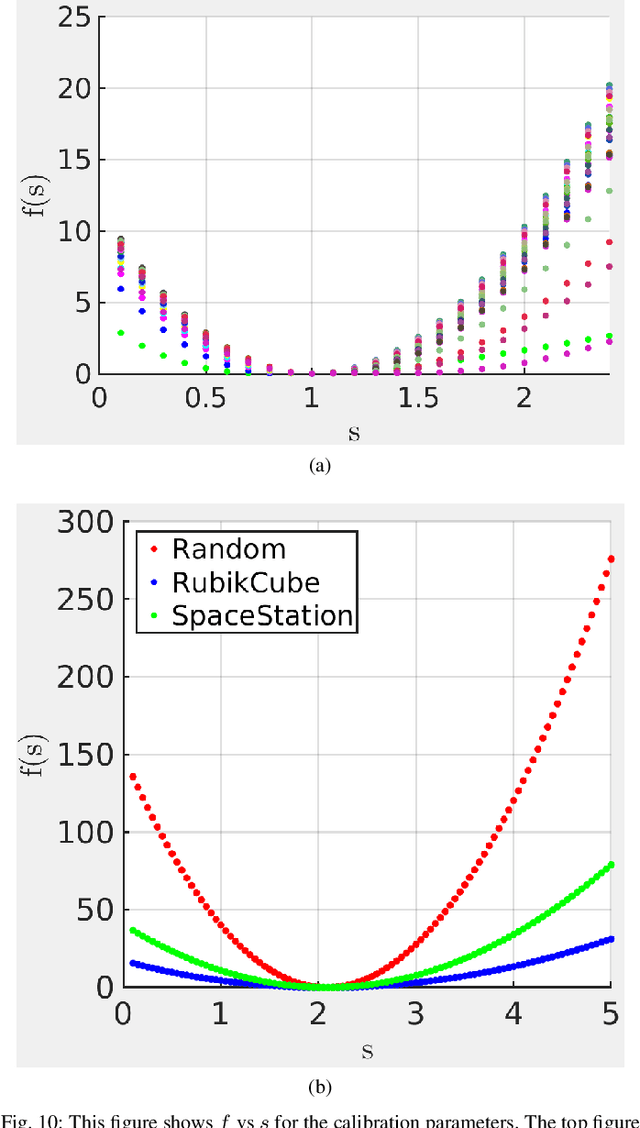
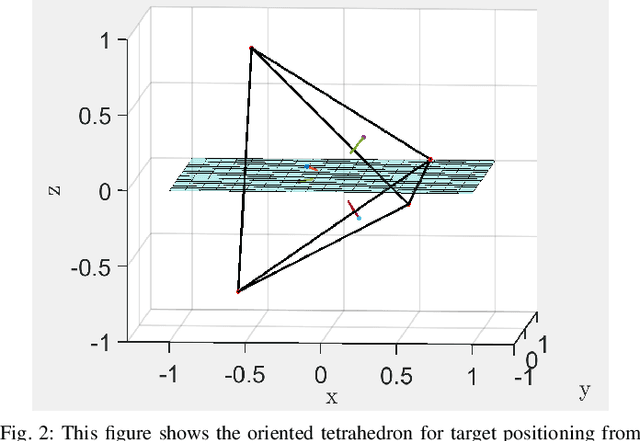
Abstract:Sensor calibration, which can be intrinsic or extrinsic, is an essential step to achieve the measurement accuracy required for modern perception and navigation systems deployed on autonomous robots. To date, intrinsic calibration models for spinning LiDARs have been based on hypothesized based on their physical mechanisms, resulting in anywhere from three to ten parameters to be estimated from data, while no phenomenological models have yet been proposed for solid-state LiDARs. Instead of going down that road, we propose to abstract away from the physics of a LiDAR type (spinning vs solid-state, for example), and focus on the spatial geometry of the point cloud generated by the sensor. By modeling the calibration parameters as an element of a special matrix Lie Group, we achieve a unifying view of calibration for different types of LiDARs. We further prove mathematically that the proposed model is well-constrained (has a unique answer) given four appropriately orientated targets. The proof provides a guideline for target positioning in the form of a tetrahedron. Moreover, an existing Semidefinite programming global solver for SE(3) can be modified to compute efficiently the optimal calibration parameters. For solid state LiDARs, we illustrate how the method works in simulation. For spinning LiDARs, we show with experimental data that the proposed matrix Lie Group model performs equally well as physics-based models in terms of reducing the P2P distance, while being more robust to noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge