Information theory for model reduction in stochastic dynamical systems

Model reduction is the construction of simple yet predictive descriptions of the dynamics of many-body systems in terms of a few relevant variables. A prerequisite to model reduction is the identification of these relevant variables, a task for which no general method exists. Here, we develop a systematic approach based on the information bottleneck to identify the relevant variables, defined as those most predictive of the future. We elucidate analytically the relation between these relevant variables and the eigenfunctions of the transfer operator describing the dynamics. Further, we show that in the limit of high compression, the relevant variables are directly determined by the slowest-decaying eigenfunctions. Our information-based approach indicates when to optimally stop increasing the complexity of the reduced model. Further, it provides a firm foundation to construct interpretable deep learning tools that perform model reduction. We illustrate how these tools work on benchmark dynamical systems and deploy them on uncurated datasets, such as satellite movies of atmospheric flows downloaded directly from YouTube.

Training Deep Neural Networks by optimizing over nonlocal paths in hyperparameter space

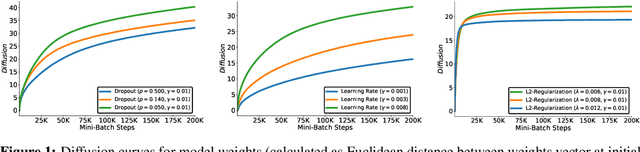
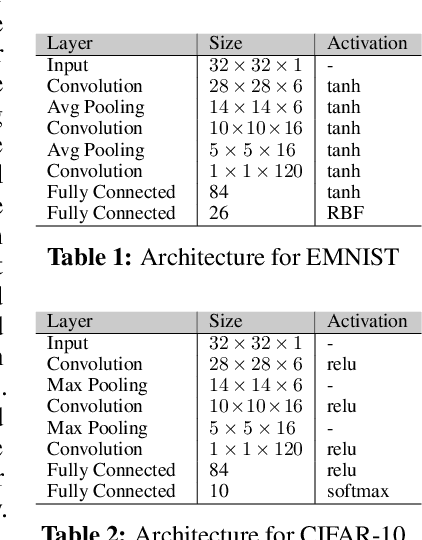
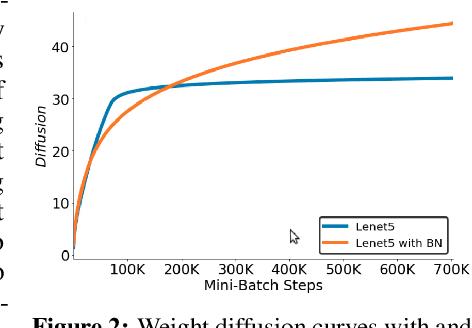
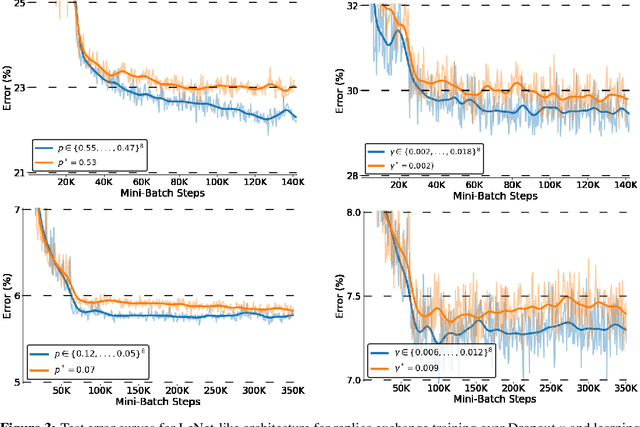
Hyperparameter optimization is both a practical issue and an interesting theoretical problem in training of deep architectures. Despite many recent advances the most commonly used methods almost universally involve training multiple and decoupled copies of the model, in effect sampling the hyperparameter space. We show that at a negligible additional computational cost, results can be improved by sampling nonlocal paths instead of points in hyperparameter space. To this end we interpret hyperparameters as controlling the level of correlated noise in training, which can be mapped to an effective temperature. The usually independent instances of the model are coupled and allowed to exchange their hyperparameters throughout the training using the well established parallel tempering technique of statistical physics. Each simulation corresponds then to a unique path, or history, in the joint hyperparameter/model-parameter space. We provide empirical tests of our method, in particular for dropout and learning rate optimization. We observed faster training and improved resistance to overfitting and showed a systematic decrease in the absolute validation error, improving over benchmark results.

Mutual Information, Neural Networks and the Renormalization Group

Physical systems differring in their microscopic details often display strikingly similar behaviour when probed at macroscopic scales. Those universal properties, largely determining their physical characteristics, are revealed by the powerful renormalization group (RG) procedure, which systematically retains "slow" degrees of freedom and integrates out the rest. However, the important degrees of freedom may be difficult to identify. Here we demonstrate a machine learning algorithm capable of identifying the relevant degrees of freedom and executing RG steps iteratively without any prior knowledge about the system. We introduce an artificial neural network based on a model-independent, information-theoretic characterization of a real-space RG procedure, performing this task. We apply the algorithm to classical statistical physics problems in one and two dimensions. We demonstrate RG flow and extract the Ising critical exponent. Our results demonstrate that machine learning techniques can extract abstract physical concepts and consequently become an integral part of theory- and model-building.