Flower Pollination Algorithm: A Novel Approach for Multiobjective Optimization

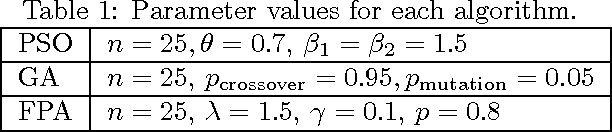
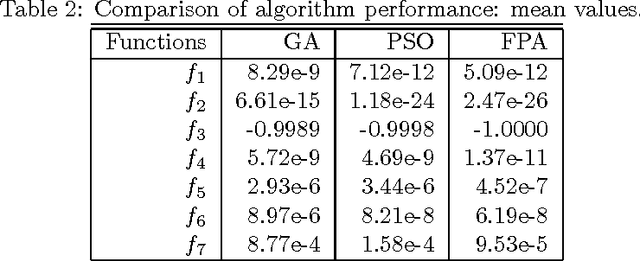
Multiobjective design optimization problems require multiobjective optimization techniques to solve, and it is often very challenging to obtain high-quality Pareto fronts accurately. In this paper, the recently developed flower pollination algorithm (FPA) is extended to solve multiobjective optimization problems. The proposed method is used to solve a set of multobjective test functions and two bi-objective design benchmarks, and a comparison of the proposed algorithm with other algorithms has been made, which shows that FPA is efficient with a good convergence rate. Finally, the importance for further parametric studies and theoretical analysis are highlighted and discussed.

Applications and Analysis of Bio-Inspired Eagle Strategy for Engineering Optimization

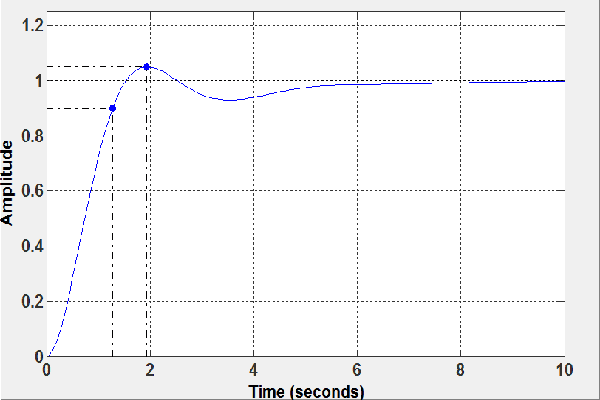
All swarm-intelligence-based optimization algorithms use some stochastic components to increase the diversity of solutions during the search process. Such randomization is often represented in terms of random walks. However, it is not yet clear why some randomization techniques (and thus why some algorithms) may perform better than others for a given set of problems. In this work, we analyze these randomization methods in the context of nature-inspired algorithms. We also use eagle strategy to provide basic observations and relate step sizes and search efficiency using Markov theory. Then, we apply our analysis and observations to solve four design benchmarks, including the designs of a pressure vessel, a speed reducer, a PID controller and a heat exchanger. Our results demonstrate that eagle strategy with L\'evy flights can perform extremely well in reducing the overall computational efforts.

Multi-objective Flower Algorithm for Optimization

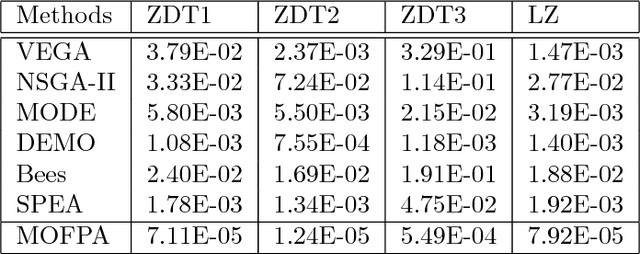
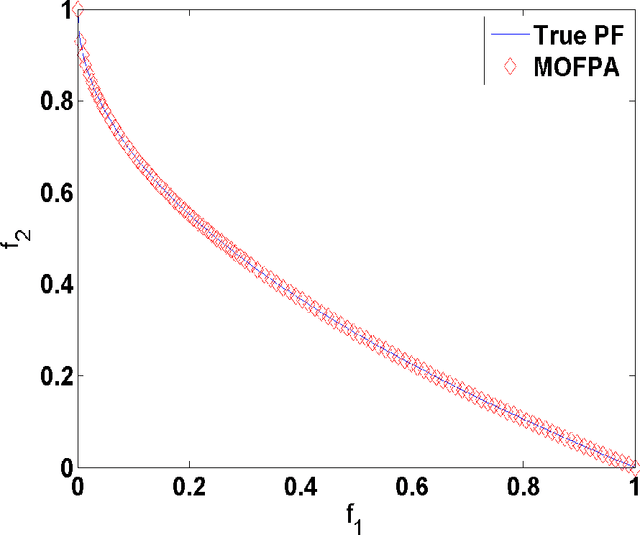
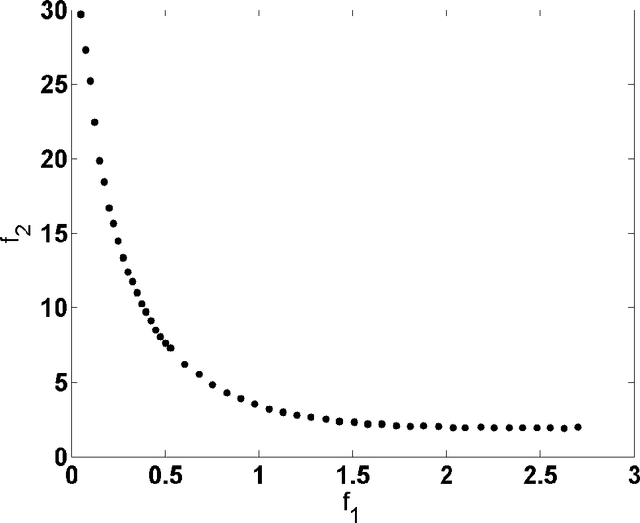
Flower pollination algorithm is a new nature-inspired algorithm, based on the characteristics of flowering plants. In this paper, we extend this flower algorithm to solve multi-objective optimization problems in engineering. By using the weighted sum method with random weights, we show that the proposed multi-objective flower algorithm can accurately find the Pareto fronts for a set of test functions. We then solve a bi-objective disc brake design problem, which indeed converges quickly.