The Alternating-Time μ-Calculus With Disjunctive Explicit Strategies

Alternating-time temporal logic (ATL) and its extensions, including the alternating-time $\mu$-calculus (AMC), serve the specification of the strategic abilities of coalitions of agents in concurrent game structures. The key ingredient of the logic are path quantifiers specifying that some coalition of agents has a joint strategy to enforce a given goal. This basic setup has been extended to let some of the agents (revocably) commit to using certain named strategies, as in ATL with explicit strategies (ATLES). In the present work, we extend ATLES with fixpoint operators and strategy disjunction, arriving at the alternating-time $\mu$-calculus with disjunctive explicit strategies (AMCDES), which allows for a more flexible formulation of temporal properties (e.g. fairness) and, through strategy disjunction, a form of controlled nondeterminism in commitments. Our main result is an ExpTime upper bound for satisfiability checking (which is thus ExpTime-complete). We also prove upper bounds QP (quasipolynomial time) and NP $\cap$ coNP for model checking under fixed interpretations of explicit strategies, and NP under open interpretation. Our key technical tool is a treatment of the AMCDES within the generic framework of coalgebraic logic, which in particular reduces the analysis of most reasoning tasks to the treatment of a very simple one-step logic featuring only propositional operators and next-step operators without nesting; we give a new model construction principle for this one-step logic that relies on a set-valued variant of first-order resolution.

Common Knowledge of Abstract Groups

Epistemic logics typically talk about knowledge of individual agents or groups of explicitly listed agents. Often, however, one wishes to express knowledge of groups of agents specified by a given property, as in `it is common knowledge among economists'. We introduce such a logic of common knowledge, which we term abstract-group epistemic logic (AGEL). That is, AGEL features a common knowledge operator for groups of agents given by concepts in a separate agent logic that we keep generic, with one possible agent logic being ALC. We show that AGEL is EXPTIME-complete, with the lower bound established by reduction from standard group epistemic logic, and the upper bound by a satisfiability-preserving embedding into the full $\mu$-calculus. Further main results include a finite model property (not enjoyed by the full $\mu$-calculus) and a complete axiomatization.

Automata Learning: An Algebraic Approach

We propose a generic categorical framework for learning unknown formal languages of various types (e.g. finite or infinite words, trees, weighted and nominal languages). Our approach is parametric in a monad T that represents the given type of languages and their recognizing algebraic structures. Using the concept of an automata presentation of T-algebras, we demonstrate that the task of learning a T-recognizable language can be reduced to learning an abstract form of automaton, which is achieved via a generalized version of Angluin's L* algorithm. The algorithm is phrased in terms of categorically described extension steps; we provide for a generic termination and complexity analysis based on a dedicated notion of finiteness. Our framework applies to structures like tree languages or omega-regular languages that were not within the scope of existing categorical accounts of automata learning. In addition, it yields new generic learning algorithms for several types of languages for which no such algorithms were previously known at all, including sorted languages, nominal languages with name binding, and cost functions.

Trichotomic Argumentation Representation

The Aristotelian trichotomy distinguishes three aspects of argumentation: Logos, Ethos, and Pathos. Even rich argumentation representations like the Argument Interchange Format (AIF) are only concerned with capturing the Logos aspect. Inference Anchoring Theory (IAT) adds the possibility to represent ethical requirements on the illocutionary force edges linking locutions to illocutions, thereby allowing to capture some aspects of ethos. With the recent extensions AIF+ and Social Argument Interchange Format (S-AIF), which embed dialogue and speakers into the AIF argumentation representation, the basis for representing all three aspects identified by Aristotle was formed. In the present work, we develop the Trichotomic Argument Interchange Format (T-AIF), building on the idea from S-AIF of adding the speakers to the argumentation graph. We capture Logos in the usual known from AIF+, Ethos in form of weighted edges between actors representing trust, and Pathos via weighted edges from actors to illocutions representing their level of commitment to the propositions. This extended structured argumentation representation opens up new possibilities of defining semantic properties on this rich graph in order to characterize and profile the reasoning patterns of the participating actors.

Integrating Generic Sensor Fusion Algorithms with Sound State Representations through Encapsulation of Manifolds

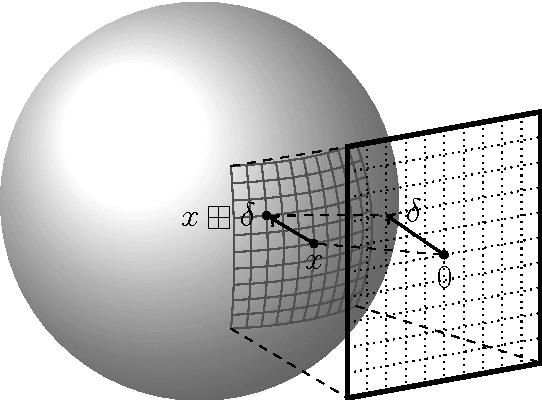
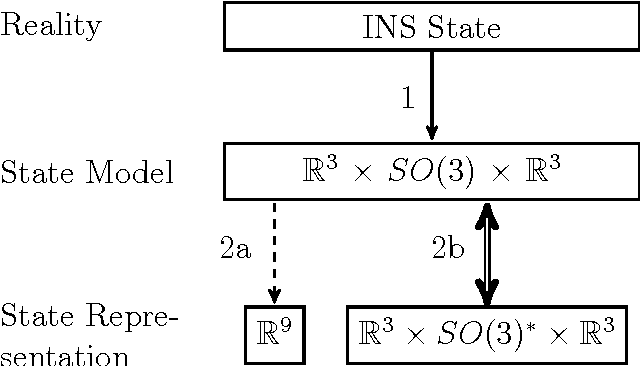
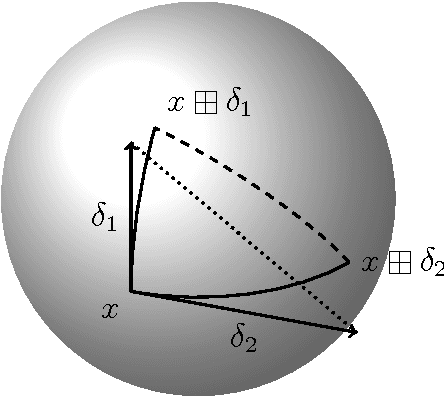
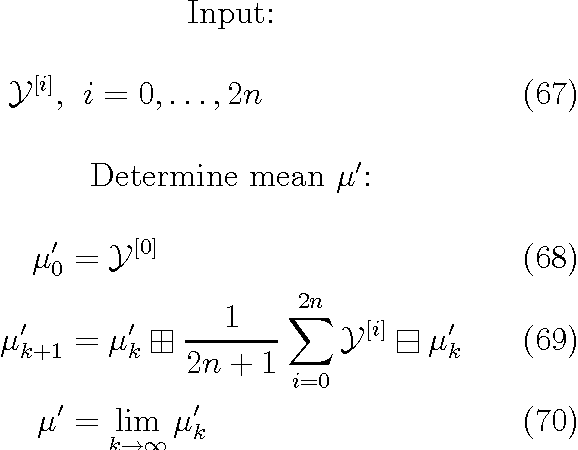
Common estimation algorithms, such as least squares estimation or the Kalman filter, operate on a state in a state space S that is represented as a real-valued vector. However, for many quantities, most notably orientations in 3D, S is not a vector space, but a so-called manifold, i.e. it behaves like a vector space locally but has a more complex global topological structure. For integrating these quantities, several ad-hoc approaches have been proposed. Here, we present a principled solution to this problem where the structure of the manifold S is encapsulated by two operators, state displacement [+]:S x R^n --> S and its inverse [-]: S x S --> R^n. These operators provide a local vector-space view \delta; --> x [+] \delta; around a given state x. Generic estimation algorithms can then work on the manifold S mainly by replacing +/- with [+]/[-] where appropriate. We analyze these operators axiomatically, and demonstrate their use in least-squares estimation and the Unscented Kalman Filter. Moreover, we exploit the idea of encapsulation from a software engineering perspective in the Manifold Toolkit, where the [+]/[-] operators mediate between a "flat-vector" view for the generic algorithm and a "named-members" view for the problem specific functions.

Shallow Models for Non-Iterative Modal Logics

The methods used to establish PSPACE-bounds for modal logics can roughly be grouped into two classes: syntax driven methods establish that exhaustive proof search can be performed in polynomial space whereas semantic approaches directly construct shallow models. In this paper, we follow the latter approach and establish generic PSPACE-bounds for a large and heterogeneous class of modal logics in a coalgebraic framework. In particular, no complete axiomatisation of the logic under scrutiny is needed. This does not only complement our earlier, syntactic, approach conceptually, but also covers a wide variety of new examples which are difficult to harness by purely syntactic means. Apart from re-proving known complexity bounds for a large variety of structurally different logics, we apply our method to obtain previously unknown PSPACE-bounds for Elgesem's logic of agency and for graded modal logic over reflexive frames.